Teorema di Bolzano Weierstrass

In una successione limitata a_n esiste almeno una successione estratta convergente.

Dimostrazione

Se una successione è limitata, allora esistono due numeri reali a e b tali che

$$ a \le a_n \le b $$

I numeri a e b sono il minimo e il massimo della successione (o viceversa).

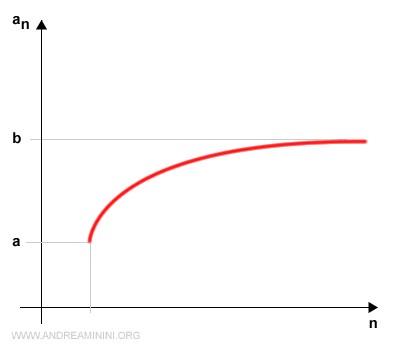
Questi due punti delimitano un insieme che contiene gli infiniti termini a_n della successione in un intervallo chiuso [a,b] sulle ordinate (asse y).

Sulle ascisse (asse x) è invece indicato l'indice n della successione.

Nota. Una successione a_n è composta da infiniti termini perché l'indice n è composto da numeri naturali e l'insieme dei numeri naturali N è infinito.

Suddivido l'intervallo [a,b] in due parti uguali identificando un punto di mezzo c=(a+b)/2.

Ora gli intervalli sono due: [a,c],[c,b]

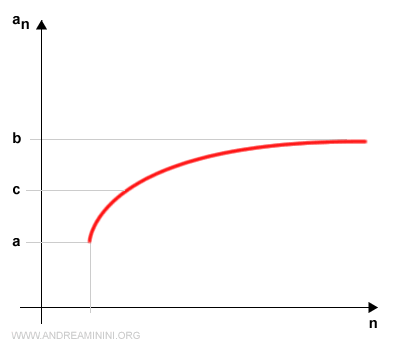
Soltanto uno dei due sottointervalli contiene infiniti termini della successione. L'altro ne contiene un numero finito.

Per ipotesi, l'intervallo [c,b] contiene infiniti termini della successione.

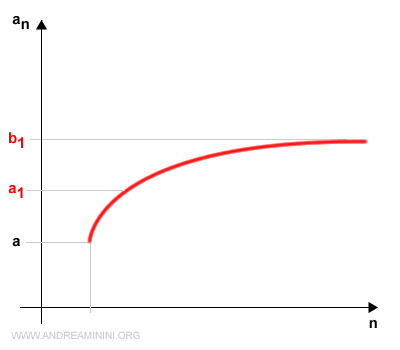
Riassegno a questo intervallo le lettere a₁ e b₁

$$ [c,b] = [a_1, b_1] $$

Qualuque sia l'intervallo scelto tra [a,c] e [c,b] valgono comunque le seguenti diseguaglianze:

$$ a \le a_1 $$ $$ b_1 \le b $$

e la lunghezza del sottointervallo è sicuramente pari alla metà del precedente

$$ b_1 - a_1 = \frac{b-a}{2} $$

Indico con n₁ il primo indice della successione a_n nell'intervallo [a₁,b₁].

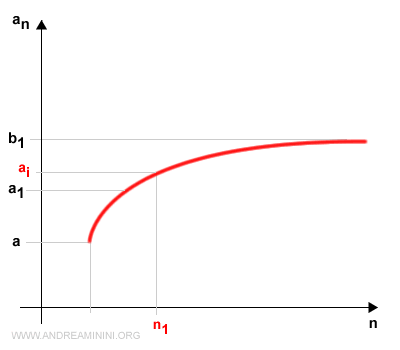
Ora suddivido l'intervallo [a₁,b₁] in due parti [a₁,c₁] e [c₁,b₁].

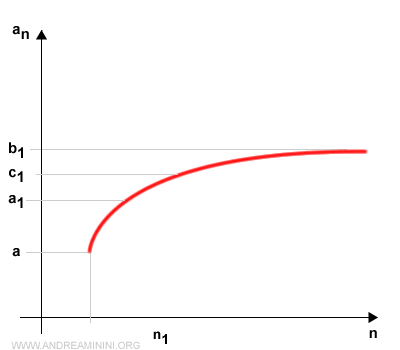
Uno dei due intervalli contiene infiniti termini (indici) della successione.

Per ipotesi, l'intervallo [c₁,b₁] contiene infiniti termini della successione.

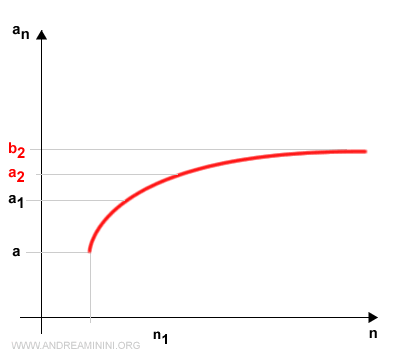
Riassegno a questo intervallo le lettere a₂ e b₂

$$ [c_1,b_1] = [a_2, b_2] $$

Anche in questo caso valgono le diseguaglianze

$$ a_1 \le a_2 $$ $$ b_2 \le b_1 $$

e la lunghezza del sottointervallo è sicuramente pari alla metà del precedente che a sua volta è la metà del precedente

$$ b_2 - a_2 = \frac{b_1-a_1}{2} = \frac{b-a}{4} $$

Indico con n₂ il primo indice della successione a_n nell'intervallo [a₂,b₂].

L'indice n₂ è un numero intero maggiore di n₁.

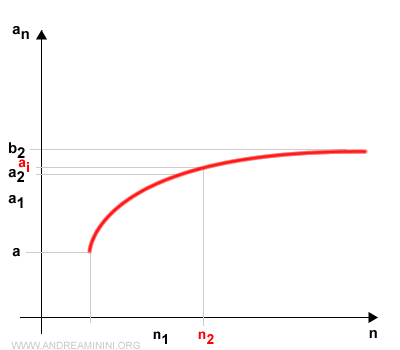
E via dicendo itero la suddivisione per k volte.

Alla fine ottengo un'unica diseguaglianza del tipo

$$ a \le a_k \le b_k \le b $$

La lunghezza dell'ultimo intervallo [a_k,b_k] è pari a all'intervallo iniziale [a,b] diviso k volte.

$$ b_k - a_k = \frac{b-a}{2^k} $$

Indico con n_k il primo indice della successione a_n nell'intervallo [a_k,b_k].

L'indice n_k è un numero intero maggiore rispetto al precedente n_k-1.

Alla fine ottengo una successione di primi numeri n

$$ n_1, n_2, .... , n_{k-1}, n_k $$

Essendo degli indici della successione a_n, i numeri n sono numeri naturali (interi).

Ogni indice n_k è un numero intero maggiore rispetto al precedente indice n_k-1.

$$ n_1< n_2< .... < n_{k-1}< n_k $$

a questi indici è associata una successione estratta da a_n

$$ a_{n_1}, a_{n_2}, .... , a_{n_k} $$

Ogni termine della successione a_nk è compreso in un intervallo [a_k,b_k].

$$ a_{n_k} \in [a_k, b_k ] $$

Quindi vale la diseguaglianza

$$ a_k \le a_{n_k} \le b_k $$

Da questo ragionamento emergono tre successioni estratte

• la successione dei termini a_k ( estremo inferiore di ogni sottointervallo [a_k,b_k] )
• il primo elemento a_nk di ogni sottointervallo [a_k,b_k]
• la successione dei termini b_k ( estremo superiore di ogni sottointervallo [a_k,b_k] )

Le due successioni estratte a_k, b_k sono monotone limitate composte da k termini perché

$$ a \le a_k \le b_k \le b $$

ossia

$$ a \le a_1 \le a_2 \le ... \le a_k \le b_1 \le b_2 \le ... \le b_k \le b $$

Calcolo il limite delle tre successioni per k→∞

$$ \lim_{k \rightarrow ∞} a_k \le \lim_{k \rightarrow ∞} a_{n_k} \le \lim_{k \rightarrow ∞} b_k $$

Le successioni a_k e b_k sono monotone e limitate.

Pertanto, secondo il teorema delle successioni monotone e limitate hanno entrambe un limite finito.

$$ l_1 \le \lim_{k \rightarrow ∞} a_{n_k} \le l_2 $$

In questo caso particolare i due limiti finiti l₁ e l₂ sono anche uguali ( l₁=l₂) tra loro.

$$ l \le \lim_{k \rightarrow ∞} a_{n_k} \le l $$

Spiegazione. Sapendo che $$ b_k - a_k = \frac{b-a}{2^k} $$ allora la successione b_k è uguale a $$ b_k = a_k + \frac{b-a}{2^k} $$ Il limite per k→∞ della successone b_k è uguale al limite di a_k. $$ l_2 = \lim_{k \rightarrow ∞} b_k = \lim_{k \rightarrow ∞} a_k + \frac{b-a}{2^k} = \lim_{k \rightarrow ∞} a_k + \lim_{k \rightarrow ∞} \frac{b-a}{2^k} = \lim_{k \rightarrow ∞} a_k + 0 = l_1 $$ perché la componente (b-a)/2^k tende a zero per k→∞.

Secondo il teorema del confronto (o teorema dei carabinieri) anche la successione a_nk intermedia ha un limite finito ed è uguale a l.

$$ \lim_{k \rightarrow ∞} a_{n_k} = l $$

Pertanto, la successione estratta a_nk è convergente.

Questo dimostra il teorema di Bolzano-Weierstrass.

E così via.