Il teorema di Bolzano

Secondo il teorema di esistenza degli zeri ( o teorema di Bolzano) in una funzione f(x) continua in un intervallo [a,b] con f(a)<0 e f(b)>0 esiste un punto intermedio x₀ in (a,b) tale che f(x₀)=0 ossia esiste una radice.

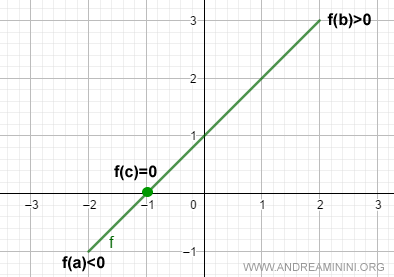
Il teorema vale anche nel caso inverso, quando f(a)>0 e f(b)<0.

Per la validità del teorema, l'importante è che la funzione abbia un segno diverso ai suoi estremi f(a) e f(b).

Un esempio pratico

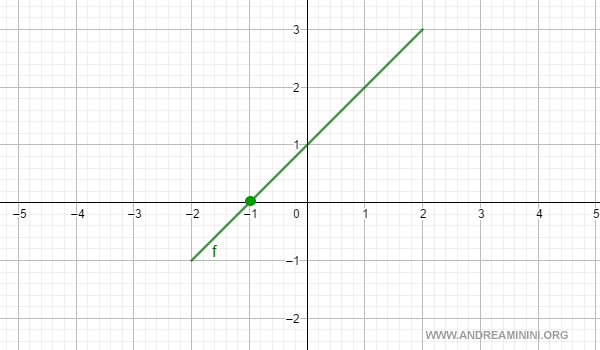
Prendo in considerazione la funzione

$$ f(x) = x+1 $$

nell'intervallo chiuso [-2,+2].

Nel punto intermedio x₀=-1 la funzione è uguale a zero.

$$ f(-1)=0 $$

E' un semplice esempio ma fa chiarezza sul significato del teorema.

La dimostrazione con spiegazione

Ho una funzione f(x) continua in [a,b].

Agli estremi la funzione assume un segno discorde.

$$ f(a)<0 $$

$$ f(b)>0 $$

Prendo in considerazione un punto c in mezzo all'intervallo [a,b]

$$ c=\frac{a+b}{2} $$

Esempio. Prendo in considerazione l'esempio precedente. La funzione f(x)=x+1 è definita nell'intervallo [-2,2]. Dove f(a)=f(-2)=1 mentre f(b)=f(2)=3. Nel punto intermedio c=0 la funzione assume il valore f(c)=f(0)=1.

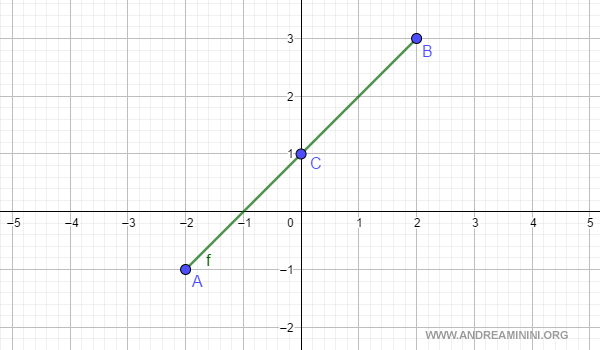
Ora analizzo il valore della funzione f(x) nel punto intermedio c

• Se f(c) è maggiore di zero $$ f(c)>0 $$ la funzione ha un segno discorde rispetto a f(a)<0. Prendo in considerazione l'intervallo [a,c]. $$ [a_1,b_1]=[a,c] $$ Poi cerco il suo punto intermedio. $$ c_2 = \frac{a_1+c_1}{2} $$ E via dicendo
• Se f(c) è minore di zero $$ f(c)<0 $$ la funzione ha un segno concorde rispetto a f(a)<0. Prendo in considerazione l'intervallo [c,b]. $$ [a_1,b_1]=[c,b] $$ Poi cerco il suo punto intermedio $$ c_2 = \frac{c_1+b_1}{2} $$ E via dicendo

Esempio. Nell'esempio precedente f(c)=1 ossia f(c)>0. Quindi, prendo come nuovo intervallo [a₁,b_1]=[a,c]. Poi individuo un nuovo punto intermedio c₁.

Ripeto l'operazione per n volte finché f(c)=0 ossia fin quando non incontro una radice. Quando f(c)=0 l'iterazione si interrompe.

Così facendo ottendo tre successioni

$$ a_n , b_n, c_n $$

Fin quando f(c)≠0 il segno della funzione è

$$ f(a_n) <0 $$ $$ f(b_n)>0 $$

Dopo ogni iterazione la lunghezza dell'intervallo [a_n,b_n] si dimezza.

$$ b_1-a_1 = \frac{b-a}{2} $$

$$ b_2-a_2 = \frac{b-a}{2^2} $$

$$ \vdots $$

Quindi dopo n iterazioni la lunghezza dell'intervallo è

$$ b_n-a_n = \frac{b-a}{2^n} $$

La successione a_n è sicuramente crescente perché

$$ a_1 \le a_2 \le ... \le a_n $$

Inoltre la successione a_n è limitata perché è contenuta nell'intervallo [a,b].

Essendo crescente e limitata, per il teorema del limite delle successioni monotone, la successione a_n ha un limite finito che chiamo x₀.

$$ \lim_{n \rightarrow ∞} a_n = x_0 $$

La successione b_n la calcolo indirettamente dall'espressione precedente.

$$ b_n-a_n = \frac{b-a}{2^n} $$

$$ b_n = a_n + \frac{b-a}{2^n} $$

Il limite della successione b_n è uguale al limite della successione a_n perché il rapporto b-a/2ⁿ tende a zero.

$$ \lim_{n \rightarrow ∞} b_n $$

$$ \lim_{n \rightarrow ∞} a_n + \frac{b-a}{2^n} = x_0 $$

Quindi, entrambe le successioni a_n e b_n convergono a x₀ per n che tende a infinito.

$$ \lim_{n \rightarrow ∞} a_n = x_0 $$

$$ \lim_{n \rightarrow ∞} b_n = x_0 $$

La successione a_n è un'approssimazione per difetto di x₀ mentre la successione b_n è un'approssimazione per eccesso di x₀.

$$ a_n \le x_0 \le b_n $$

Il valore della funzione f(x) nel punto x₀ è approssimabile al limite delle successioni a_n e b_n per n che tende a infinito.

$$ f(x_0) = \lim_{n \rightarrow ∞} f(a_n) $$

$$ f(x_0) = \lim_{n \rightarrow ∞} f(b_n) $$

Tuttavia, la prima è un'approssimazione per difetto di f(x₀) mentre la seconda è un'approssimazione per eccesso di f(x₀).

Sapendo che f(a_n)≤0 e f(b_n)≥0.

$$ f(x_0) = \lim_{n \rightarrow ∞} f(a_n) \le 0 $$

$$ f(x_0) = \lim_{n \rightarrow ∞} f(b_n) \ge 0 $$

Quindi, il valore della funzione f(x₀) deve essere uguale a zero

$$ f(x_0) = 0 $$

Questo dimostra il teorema di esistenza degli zeri.

E così via.