Il teorema di esistenza dei valori intermedi
Una funzione f(x) continua in un intervallo [a,b] assume tutti i valori compresi tra f(a) e f(b). E' anche detto teorema di tutti i valori.
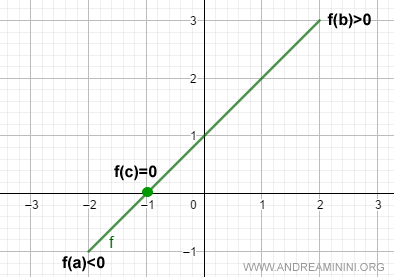
Si applica alle funzioni continue reali.
Secondo il teorema, l'immagine [f(a),f(b)] di un intervallo [a,b] contiene tutti i valori compresi tra le immagini degli estremi f(a) e f(b).
Un esempio pratico
Ho la seguente funzione continua nell'intervallo [-2,2]
$$ f(x)=x+1 $$
La funzione è negativa all'estremo sinistro a=-2 e positiva all'estremo destro b=2
$$ f(a) = f(-2)=-1 $$
$$ f(b) = f(2)=3 $$
Tra il valore f(a) e f(b) esistono tutti i valori intermedi per qualsiasi x di [a,b]
La dimostrazione con spiegazione
Prendo in considerazione una funzione continua in cui l'estremo f(a) sia inferiore all'estremo f(b).
$$ f(a) \le f(b) $$
Secondo il teorema dei valori intermedi
$$ \forall \: y_0 \in [f(a),f(b)] \: \exists \: x_0 \in [a,b] \: : \: f(x_0)=f(y_0) $$
Creo una funzione g(x) per misurare la differenza tra il valore y0 e qualsiasi altro valore di f(x) nell'intervallo [a,b]
$$ g(x) = f(x) - y \:\:\: \forall \: x \in [a,b] $$
Calcolo la funzione differenza rispetto agli estremi dell'intervallo [a,b]
$$ g(a)=f(a)-y $$
$$ g(b)=f(b)-y $$
Essendo f(a)<(b) allora il valore y0 è compreso tra questi valori estremi
$$ f(a) < y < f(b) $$
Quindi, posso calcolare il segno delle funzioni differenza.
$$ g(a)=f(a)-y < 0 $$
$$ g(b)=f(b)-y > 0 $$
La funzione g(x) ha un valore estremo negativo g(a)<0 e un valore estremo positivo g(b)>0.
Secondo il teorema di esistenza degli zeri, esiste un punto intermedio x0 in cui la funzione è nulla.
$$ f(x_0)=y $$
Essendo una funzione continua, la presenza del punto intermedio f(x0) dimostra l'esistenza dei valori intermedi tra gli estremi f(a) e f(b) per qualsiasi x di [a,b].
Corollario di esistenza tra un minimo e un massimo
Se una funzione è continua in un intervallo [a,b], la funzione assume tutti i valori possibili tra un minimo (m) e un massimo (M).
La dimostrazione
Secondo il teorema di Weierstrass una funzione continua in un intervallo chiuso [a,b] ha un valore minimo (m) e un valore massimo (M).
Devo provare che per qualsiasi valore y0 di [m,M] esiste un valore x0 di [a,b] tale che f(x0)=y0
$$ \forall \: y_0 \in (m,M) \: \exists \: x_0 \in [a,b] \: : \: f(x_0)=y_0 $$
Prendo in considerazioni il punto di minimo (x1) e il punto di massimo (x2).
$$ m=f(x_1) $$
$$ M=f(x_2) $$
Definisco una funzione differenza f(x)-y0
$$ h(x)=f(x)-y_0 $$
Poiché m<y0 la funzione h(x) è minore di zero in x1 (punto di minimo).
$$ h(x_1)=f(x_1)-y_0< 0 $$
poiché M>y0 la funzione h(x) è maggiore di zero in x2 (punto di massimo)
$$ h(x_2)=f(x_2)-y_0> 0 $$
Secondo il teorema di esistenza degli zeri, esiste un numero x0 nell'intervallo aperto (x1,x2) tale che g(x0)=0.
Se g(x0)=0 allora
$$ f(x_0)=y_0 $$
Quindi il valore y0 è uguale a f(x0) ossia esiste un punto x0 in [a,b] tale che f(x0)=y0.
Essendo la funzione f(x) continua in [m,M] lo stesso procedimento posso ripeterlo per ogni valore y0∈(m,M)
Pertanto, per ogni y0∈(m,M) del codominio esiste un punto x0 del dominio tale che f(x0)=y0.
Il teorema è dimostrato.
E così via.
