Il teorema di Weierstrass
Una funzione f(x) continua in un intervallo chiuso e limitato [a,b] ha un valore minimo m=f(x1) e massimo M=f(x2) tali che $$ f(x_1) \le f(x) \le f(x_2) \:\:\: \forall x \in [a,b] $$
I punti \( x_1 \) e \( x_2 \) dell'intervallo \([a,b]\) sono detti rispettivamente punti di minimo assoluto e di massimo assoluto.
Il teorema di Weierstrass fornisce una condizione sufficiente ma non necessaria per l'esistenza di massimo e minimo assoluti.
Questo significa che se la funzione non è continua o l'intervallo non è chiuso e limitato, potrebbero comunque esistere dei punti di massimo e minimo, ma la loro esistenza non è più garantita.
Nota. In generale, il teorema si estende anche alle funzioni di più variabili (ad esempio \( f(x,y) \)), a condizione che il dominio sia chiuso e limitato* (cioè compatto) e che la funzione sia continua su di esso.
Un esempio pratico
Prendo in considerazione questa funzione.
$$ f(x) = \frac{1}{x} $$
La funzione non è limitata nell'intervallo (0,5] perché non ha un estremo superiore. Quindi non può avere un massimo (M).
Non è limitata nemmeno nell'intervallo [5,+∞) perché pur avendo un limite che tende a zero (estremo inferiore), non esiste un numero x tale tale che f(x)=0. Quindi non ha un minimo (m).
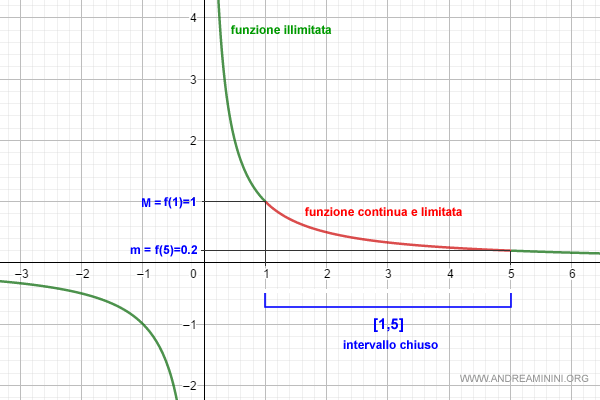
Tuttavia, se prendo in considerazione l'intervallo chiuso [1,5] la f(x) diventa una funzione limitata.
$$ 0.2 \le f(x) \le 1 \:\:\: \forall x \in [1,5] $$
In questo caso, esistono due punti di minimo (x1) e di massimo (x2) nell'intervallo [a,b] del dominio in cui la funzione assume il minimo e il massimo.
$$ M=f(1)=1 $$
$$ m=f(5)=0.2 $$
Nota. In questo caso i punti di minimo e di massimo sono gli estremi dell'intervallo chiuso [a,b]. Non è però detto. In altri casi i punti di minimo e massimo potrebbero essere anche dei punti interni nell'intervallo [a,b]. Lo specifico perché è facile confondersi.
La dimostrazione con spiegazione
Prendo in considerazione una funzione f(x) in un intervallo chiuso [a,b] in cui esiste un valore massimo M.
$$ M=sup(f(x):x \in [a,b]) $$
Esempio. Questo grafico mostra la funzione coseno nell'intervallo [-1,1]. La funzione ha un punto di massimo in x0=0 dove la f(x) assume il valore massimo M=1.
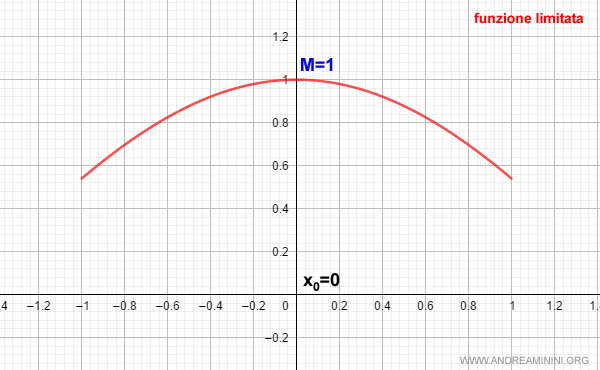
Avendo un estremo superiore (M) esiste una successione xn che fa convergere la funzione f(x) al massimo.
$$ \lim_{n \rightarrow ∞} f(x_n) = M $$
Ci sono due ipotesi:
- M è limite infinito
Se M=+∞ allora per ogni n ∈ N esiste xn in [a,b] tale che $$ f(x_n)>n $$ Quindi, il limite della successione è infinito $$ M = \lim_{n \rightarrow ∞} f(x_n) = ∞ $$ - M è limite finito
Se M<+∞ allora per ogni n ∈ N esiste xn in [a,b] tale che $$ M-\frac{1}{n} < f(x_n) \le M $$ Quindi, il limite della successione è finito $$ M = \lim_{n \rightarrow ∞} f(x_n) = f(x_0) $$
Ora devo capire se M è un numero finito o infinito.
Essendo l'intervallo [a,b] limitato, la successione xn è limitata. Quindi, per il teorema di Bolzano-Weierstrass esiste una successione estratta xnk convergente a un punto dell'intervallo [a,b].
Esempio. Un esempio di successione estratta convergente.
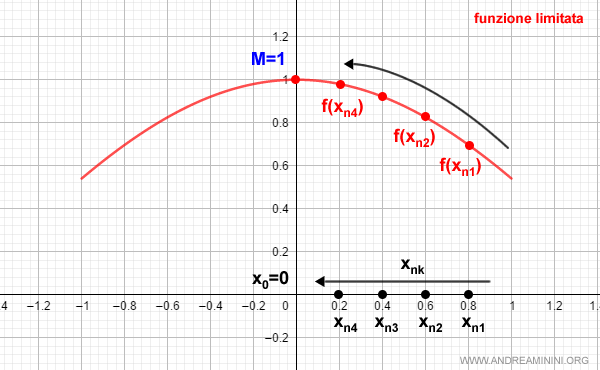
Prendo in considerazione una successione estratta xnk che converge al punto x0 dell'intervallo [a,b].
$$ \lim_{n \rightarrow ∞} x_{nk} = x_0 $$
Nota. Il punto x0 è quello in cui per ipotesi potrebbe convergere la funzione f(x) se ha un massimo limitato. $$ M = \lim_{n \rightarrow ∞} f(x_n) = f(x_0) $$
Essendo la funzione f(x) continua, la funzione f(xnk) converge a f(x0)
$$ \lim_{n \rightarrow ∞} f(x_{nk}) = f(x_0) $$
Quindi
$$ \begin{cases} M = \lim_{n \rightarrow ∞} f(x_n) = f(x_0) \\ \\ \lim_{k \rightarrow ∞} f(x_{nk}) = f(x_0) \end{cases} $$
pertanto vale la seguente uguaglianza
$$ M = \lim_{n \rightarrow ∞} f(x_n) = \lim_{k \rightarrow ∞} f(x_{nk}) = f(x_0) $$
Questo dimostra che l'estremo superiore della funzione è un massimo M finito
$$ M = f(x_0) = sup \{ f(x) \: \forall x \in [a,b] \} $$
Quindi il limite della funzione f(xn) converge a un numero finito M e non diverge a infinito
$$ \lim_{n \rightarrow \infty} f(x_n) = M $$
Nota. Posso seguire lo stesso ragionamento per determinare il punto di minimo a partire dall'estremo inferiore m=f(x) nell'intervallo chiuso [a,b].
Il teorema di Weierstrass per funzioni di due o più variabili
Sia \( A \subseteq \mathbb{R}^n \) un insieme compatto (cioè chiuso e limitato), e sia \( f : A \to \mathbb{R} \) una funzione continua. Allora \( f \) assume su \( A \) sia un valore minimo assoluto sia un valore massimo assoluto: esistono punti \( x_{\text{min}}, x_{\text{max}} \in A \) tali che\[f(x_{\text{min}}) \le f(x) \le f(x_{\text{max}}) \quad \forall x \in A.\]
E' l'estensione naturale del teorema di Weierstrass alle funzioni di più variabili.
In questo caso si parla di compattezza dell'insieme perché l'insieme del dominio deve essere sia chiuso che limitato.
Nota. Nel caso delle funzioni di una variabile $ f(x) $, il dominio considerato nel teorema di Weierstrass è un intervallo chiuso e limitato $ [a,b] $ sulla retta reale, delimitato da due estremi. Nel caso delle funzioni di due variabili $ f(x,y) $, invece, il dominio è un insieme di punti del piano $ R^2 $, ad esempio un disco chiuso $ x^2+y^2 \le r^2 $. In questo caso gli "estremi" del dominio corrispondono al bordo dell'insieme (ad esempio la circonferenza del disco).
Esempio
Considero la funzione di due variabili
\[ f(x,y) = x^2 + y^2 \]
e come dominio prendo il disco chiuso di raggio 1 centrato nell'origine degli assi (0,0).
\[ A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 1 \} \]
Il dominio \( A \) è chiuso perché contiene anche il bordo \( x^2+y^2=1 \)) e limitato peché è contenuto in un cerchio di raggio 1.
Quindi, l'insieme \( A \) è compatto.
La funzione \( f(x,y) = x^2+y^2 \) è continua su tutto \( \mathbb{R}^2 \) e quindi anche sul dominio \( A \) .
Secondo il teorema di Weierstrass la funzione \( f \) assume un massimo e un minimo assoluti su \( A \).
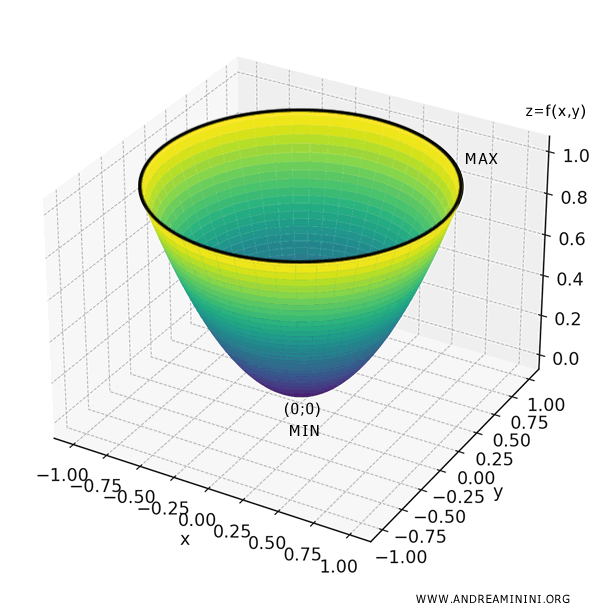
In questo caso il minimo assoluto si verifica quando \( x=0 \) e \( y=0 \), cioè al centro del disco, e vale \( f(0,0) = 0 \).
Il massimo assoluto si verifica su tutto il bordo del disco \( x^2+y^2=1 \), dove \( f(x,y) = 1 \). Quindi, non c'è un unico punto di massimo assoluto ma tanti.
E così via.
