Limiti di funzioni composte
Il limite di una funzione composta f(g(x)) per x che tende a x0 è uguale a l $$ \lim_{x \rightarrow x_0} f(g(x)) = l $$ se $$ \lim_{x \rightarrow x_0} g(x) = y_0 $$ $$ \lim_{y \rightarrow y_0} f(y) = l $$ e se esiste un δ>0 tale che $$ g(x) \ne \lim_{x \rightarrow x_0} g(x) \:\:\: \forall x \ne x0 \in (x_0-δ, x_0+δ ) $$
Se la funzione g(x) per x→x0 tende a y
$$ \lim_{x \rightarrow x_0} g(x) = y_0 $$
e la funzione f(y) per y→y0 tende a l
$$ \lim_{y \rightarrow y_0} f(y) = l $$
allora anche f(g(x)) per x→x0 tende a l
$$ \lim_{x \rightarrow x_0} f(g(x)) = l $$
Un esempio pratico
Ho la funzione f(x)
$$ f(x) = \log \frac{1}{x} $$
Si tratta di una funzione composta del tipo f(g(x)) con
$$ y = g(x) = \frac{1}{x} $$
$$ f(y) = \log y $$
Per calcolare il limite della funzione composta
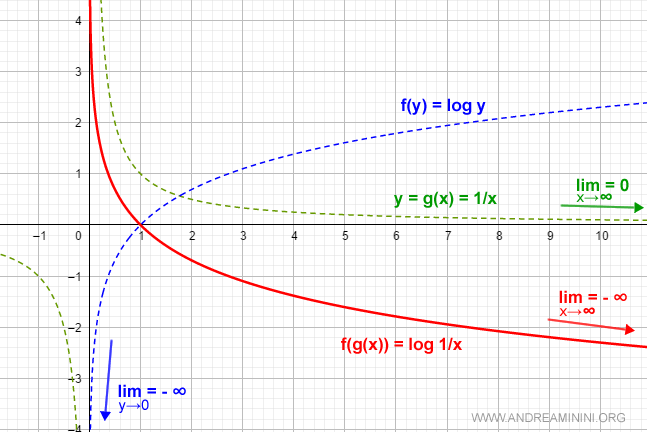
$$ \lim_{x \rightarrow ∞} \log \frac{1}{x} $$
posso scorporare il limite in due limiti.
Calcolo il limite della g(x) per x che tende a infinito
$$ y_0 = \lim_{x \rightarrow ∞} g(x) = \lim_{x \rightarrow ∞} \frac{1}{x} = 0 $$
Poi calcolo il limite della f(y) per y che tende a y0=0
$$ l = \lim_{y \rightarrow 0} f(y) = \lim_{y \rightarrow 0} \log y = -∞ $$
Il limite della funzione composta per x che tende a infinito è l=-∞.
La dimostrazione
Prendo in considerazione la funzione f(g(x)) che converge a l nel punto x0
$$ \lim_{x \rightarrow x_0} f(g(x)) = l $$
Considero una successione estratta xn dal dominio della funzione f(g(x)) che converge a x0.
$$ \lim_{n \rightarrow \infty} x_n = x_0 $$
Secondo la definizione di limite di una successione, per x che tende a x0 il limite è uguale a l se esiste un valore v tale che
$$ |x_n-x_0|<δ \:\:\: \forall n>v $$
Quindi, la successione estratta xn non contiene il termine x0.
A partire dalla successione xn calcolo una seconda successione yn tramite la funzione g(y)
$$ y_n = g(x_n) $$
Poiché la successione non contiene x0, per ogni n>v la funzione yn=g(xn) è diversa da g(x0)
$$ y_n \ne g(x_0) $$
Quindi, essendo y0=g(x0)
$$ y_n \ne y_0 \:\:\: \forall n>v $$
A sua volta il limite della successione yn tende a l
$$ lim_{n \rightarrow y_0} y_n = l $$
E così via.
