Teorema della permanenza del segno del limite di una successione
Se il limite di una successione an per n tendente a infinito converge a l maggiore di zero, allora esiste un numero v tale che per qualsiasi n>v la successione an è maggiore di 0. $$ \lim_{n \rightarrow ∞ } a_n = l>0 \rightarrow \exists \: v \: : \forall n>v \: a_n>0 $$
Un esempio pratico
Ho la successione
$$ a_n = \frac{n-3}{n} $$
I primi termini della successione sono
$$ a_1 = -2 \\ a_2 = -0.5 \\ a_3 = 0 \\ a_4 = 0.25 \\ a_5 = 0.4 \\ \vdots $$
Il limite della successione converge a +1
$$ \lim_{n \rightarrow ∞} \frac{n-3}{n} = 1 $$
Secondo il teorema della permanenza del segno esiste un valore v tale che la successione ha lo stesso segno del limite, ossia an>0, per qualsiasi n>v
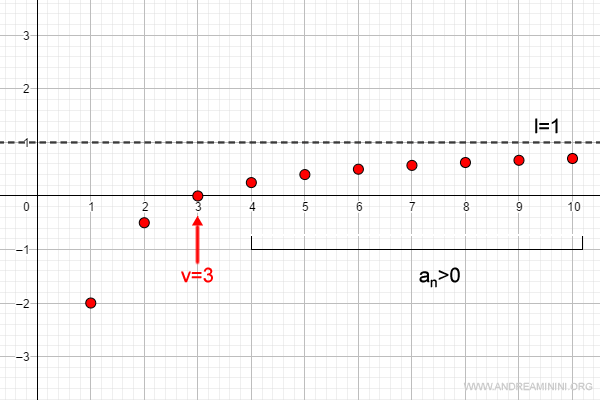
In questo esempio v=3, perché per n>v i termini della successione hanno tutti il segno positivo come il limite (1).
$$ a_4 = 0.25 \\ a_5 = 0.4 \\ \vdots $$
Attenzione. Il teorema della permanenza del segno non afferma che tutti i termini hanno lo stesso segno del limite, ma solo quelli per cui n>v. In questo esempio, i primi due termini sono negativi mentre il terzo è nullo. Solo i termini dal quarto in poi sono positivi.
La dimostrazione
Se il limite (l) della successione è maggiore di zero (l>0).
$$ \lim_{n \rightarrow ∞} a_n = l > 0 $$
Allora esiste un valore ε>0 tale che
$$ | a_n - l | < ε $$
Scelgo come valore di riferimento ε=l/2
$$ | a_n - l | < \frac{l}{2} $$
Secondo il teorema della permanenza del segno esiste un valore v tale che
$$ | a_n - l | < \frac{l}{2} \:\:\:\: \forall \ n>v $$
Questo equivale a dire
$$ - \frac{l}{2} < a_n - l < \frac{l}{2} $$
$$ l - \frac{l}{2} < a_n < l + \frac{l}{2} $$
$$ \frac{2l-l}{2} < a_n < \frac{2l+l}{2} $$
$$ \frac{l}{2} < a_n < \frac{3l}{2} $$
Prendo in considerazione soltanto
$$ \frac{l}{2} < a_n $$
Essendo l>0 per ipotesi allora anche l/2 è maggiore di zero
$$ 0 < \frac{l}{2} < a_n $$
Quindi
$$ 0 < a_n $$
ossia
$$ a_n > 0 $$
Questo dimostra che i termini della successione dopo v sono tutti positivi.
Pertanto, permane il segno del limite per ogni n>v.
Alcuni corollari utili
Corollario 1
Se un limite per n tendente a infinito ha tutti i termini della successione non negativi an≥0, allora anche il limite della successione è un numero non negativo l≥0 $$ \forall n>0 : a_n≥0 \Rightarrow \lim_{n \rightarrow ∞} a_n = l ≥ 0 $$
Lo stesso discorso vale anche al contrario, se i termini della successione sono tutti non positivi, allora anche il limite è un numero non positivo.
Dimostrazione
Ho una successione con tutti i termini maggiori o uguali a zero
$$ a_n>0 \:\:\: \forall n≥0 $$
Se per assurdo il limite (l) della successione fosse negativo
$$ \lim_{n \rightarrow ∞} a_n = l < 0 $$
allora per il teorema della permanenza del segno dovrebbe esistere un elemento v>0 tale che an<0 per ogni n>v
$$ \exists v>0 \:\: | \:\: a_n<0 \:\:\: \forall n>0 $$
Questo è però impossibile perché tutti gli elementi della successione sono non negativi an≥0 per l'ipotesi iniziale.
Quindi, il teorema della permanenza del segno non sarebbe soddisfatto se il limite fosse negativo.
Se il limite non può essere negativo, allora deve essere maggiore o uguale a zero.
Questo dimostra il corollario.
Corollario 2
Date due successioni an e bn limitate rispettivamente a la e lb, se i termini della successione sono an≥bn per ogni n>0, allora anche i limiti delle successioni sono la≥lb. $$ \forall n>0 \:\: a_n≥b_n \: \Rightarrow \: l_a≥l_b $$
Dimostrazione
Ho due successioni an e bn limitate a la e lb
$$ l_a= \lim_{n \rightarrow ∞} a_n $$ $$ l_b= \lim_{n \rightarrow ∞} b_n $$
Per ipotesi, ogni termine della successione an è maggiore uguale al corrispettivo termine della successione bn
$$ a_n \ge b_n $$
Pertanto
$$ a_n - b_n \ge 0 $$
e anche il limite della differenza è maggiore o uguale a zero
$$ \lim_{n \rightarrow ∞} a_n-b_n \ge 0 $$
Se per assurdo il limite della differenza an-bn fosse negativo, secondo il teorema della permanenza del segno dovrebbe esistere un numero v>0 tale che an-bn<0 ossia an<bn.
Questo però è impossibile per l'ipotesi iniziale. Quindi, il teorema della permanenza del segno non sarebbe rispettato.
Pertanto, se il limite della differenza an-bn non può essere negativo, allora deve essere necessariamente maggiore o uguale a zero an-bn≥0 ossia an≥bn.
Questo dimostra il corollario.
E così via.
