Il teorema del limite delle successioni monotone
Una successione monotona ha sempre un limite finito o infinito. $$ \lim_{n \rightarrow ∞} a_n = \begin{cases} l \\ ∞ \end{cases} $$ Se la successione monotona è anche limitata, allora la successione è convergente a un limite finito. $$ \lim_{n \rightarrow ∞} a_n = l $$
Ogni successione monotona è anche una successione regolare, perché ammette sempre un limite finito.
Il significato di monotòna, regolare e limitata. Una successione è detta monotòna se ogni suo termine an è sempre maggiore-uguale o minore-uguale al successivo termine an+1. Se è maggiore o minore è detta strettamente monotòna. La successione è detta regolare se ammette un limite finito o infinito. La successione è detta limitata se ha un limite finito.
Esempi pratici
Esempio 1
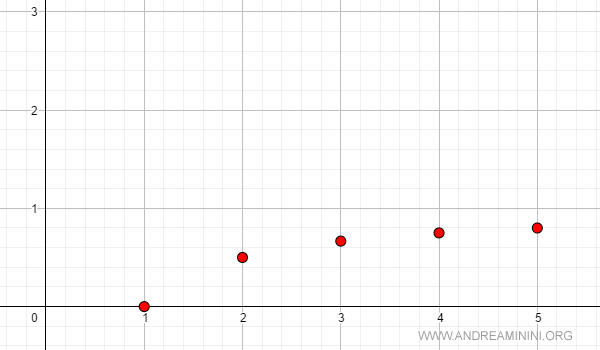
Questa successione è monotona crescente ed è limitata
$$ a_n = \frac{n-1}{n} $$
Il limite della successione converge a 1.
$$ \lim_{n \rightarrow ∞} a_n = 1 $$
Ecco la rappresentazione grafica
Esempio 2
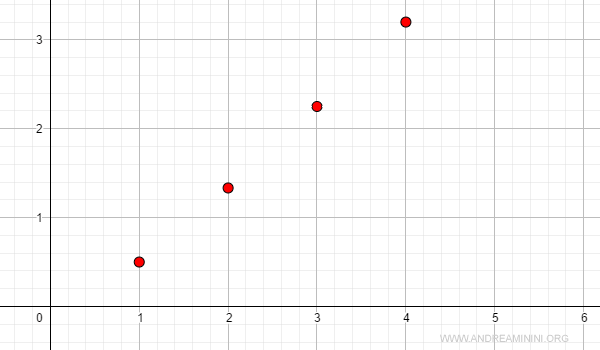
Questa successione è monotona crescente ma non è limitata
$$ a_n = \frac{n^2}{n+1} $$
Il limite della successione è infinito.
$$ \lim_{n \rightarrow ∞} a_n = +∞ $$
Ecco la rappresentazione grafica
La dimostrazione
Per dimostrare il teorema analizzo due casi. Nel primo caso la successione monotona è limitata mentre nel secondo caso è illimitata.
Ipotesi 1 (successione limitata e crescente)
Ho una successione monotòna limitata e crescente.
Fissato un ε>0 esiste un valore v tale che per ogni n>v
$$ l-ε < a_v \le a_n \le l < l+ε $$
Sul diagramma cartesiano la diseguaglianza diventa è più chiara
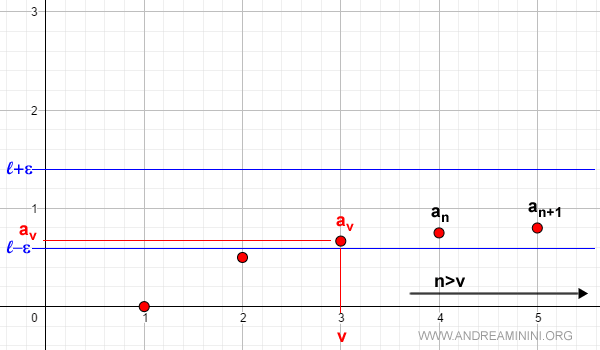
Pertanto, per n tendente a infinito la successione converge a l=1
$$ \lim_{n \rightarrow ∞} a_n = 1 $$
Ipotesi 2 (successione non limitata e crescente)
Ho una successione monotona crescente illimitata.
Non avendo un limite superiore, fissato un M>0 esiste un valore v>0 tale che per ogni n>v vale
$$ a_n \ge a_v > M $$
Guardandola su un diagramma cartesiano la diseguaglianza è molto più comprensibile.
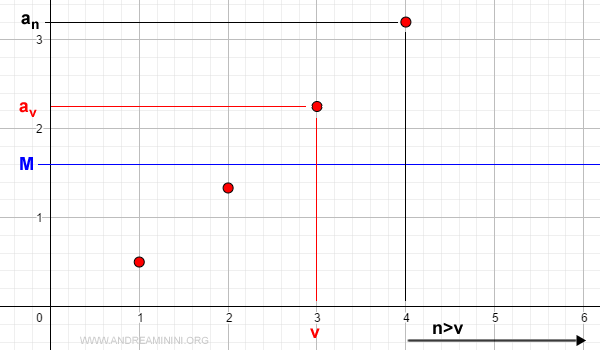
Pertanto, per n tendente a infinito la successione tende a infinito
$$ \lim_{n \rightarrow ∞} a_n = +∞ $$
Nota. La dimostrazione delle successioni monotone decrescenti, limitate e non limitate, è simile a quella delle successioni crescenti.
E così via.
