Il teorema sul limite di una funzione monotona
Una funzione f(x) monotòna nell'intervallo chiuso [a,b] ha limiti finiti per ogni punto x0 di (a,b) $$ \lim_{x \rightarrow x_0^-} = l \\ \lim_{x \rightarrow x_0^+} = l $$ e limite destro finito per l'estremo iniziale $$ \lim_{x \rightarrow a^+} = l_a $$ e limite sinistro finito per l'estremo finale $$ \lim_{x \rightarrow b^-} = l_b $$
Per limite "finito" si intende un numero qualsiasi (non infinito).
Cos'è una funzione monotòna? Una funzione è detta monotòna se in ogni punto è sempre crescente o sempre decrescente.
Un esempio pratico
La funzione f(x)=x3 nell'intervallo [-1,1] è una funzione monotona crescente.
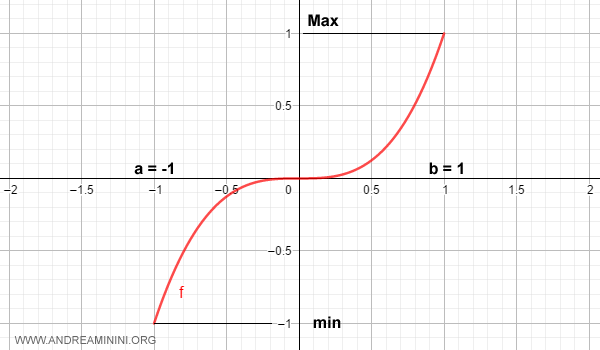
In ogni punto x0 dell'intervallo (-1,1) esiste il limite finito per x che tende a x0
Quindi, il limite destro e sinistro coincidono.
$$ \lim_{x \rightarrow x_0^-} x^3 = \lim_{x \rightarrow x_0^+} x^3 = f(x_0) $$
Nell'estremo a=-1 esiste il limite finito destro per x→a
$$ \lim_{x \rightarrow a^+} x^3 = f(a) $$
mentre nell'estremo b=1 esiste il limite finito sinistro per x→b
$$ \lim_{x \rightarrow a^-} x^3 = f(b) $$
La dimostrazione con spiegazione
Prendo in considerazione una funzione f(x) crescente nell'intervallo chiuso [a,b].
Essendo una funzione crescente in un intervallo chiuso, la funzione ammette un minimo f(a) e un massimo f(b)
Esempio. La funzione f(x)=x/2 è monotona crescente nell'intervallo chiuso [2,6] e ammette un minimo f(2)=1 e un massimo f(b)=3.
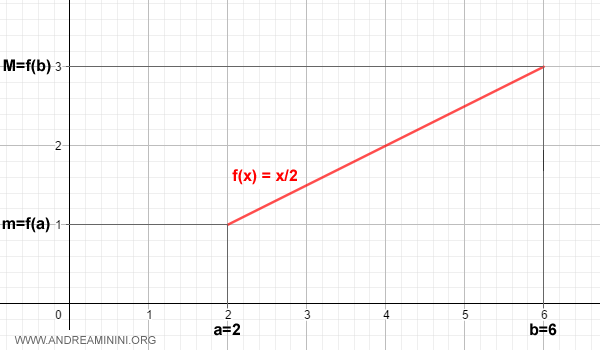
Quindi, ogni valore f(x) è compreso tra f(a) e f(b).
$$ f(a) \le f(x) \le f(b) \:\: \forall x \in [a,b] $$
Analizzo un generico punto x0 nell'intervallo (a,b], escludendo il valore minimo
Poi cerco l'estremo superiore nell'intervallo [a,x0), tra il punto di minimo (a) incluso e il punto x0 escluso.
$$ l' = sup( f(x):x \in [a,x_0) ) $$
Essendo una funzione monotona con un massimo finito, anche l'estremo superiore l' deve essere un numero finito.
Esempio
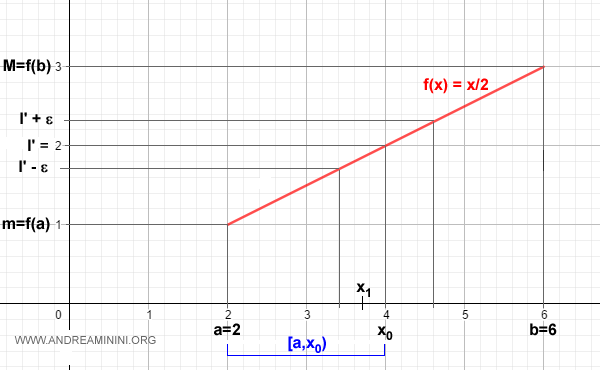
In una funzione continua monotona, per ogni ε>0 esiste un x1 di [a,x0) tale che
$$ l'-ε < f(x_1) $$
Considero anche l'esistenza dell'estremo superiore l'
$$ l'-ε < f(x_1) \le l' < l'+ε $$
Quindi, in una funzione crescente per ogni x>x1 posso affermare che
$$ l'-ε < f(x_1) \le f(x) \le l' < l'+ε \:\:\: \forall x>x_1 $$
Questo vuol dire che esiste un limite finito verso il punto x0 da sinistra.
$$ \lim_{x \rightarrow x_0^-} f(x) = l' $$
Seguendo lo stesso procedimento scelgo un punto x0 nell'intervallo (x0,b].
Poi individuo l'estremo inferiore.
$$ l' = inf( f(x):x \in (x_0,b] ) $$
Essendo una funzione monotona con un minimo finito, anche l'estremo inferiore l' deve essere un numero finito.
Per ogni ε>0 esiste un x1 di (x0,b] tale che
$$ l'+ε > f(x_1) $$
Considero anche l'esistenza dell'estremo inferiore l'
$$ l'+ε > f(x_1) \ge l' > l'-ε $$
Quindi, in una funzione crescente per ogni x<x1 posso affermare che
$$ l'+ε > f(x_1) \ge f(x) \ge l' > l'-ε \:\:\: \forall x<x_1 $$
Questo vuol dire che esiste un limite finito verso il punto x0 da destra.
$$ \lim_{x \rightarrow x_0^+} f(x) = l' $$
Essendoci sia il limite sinistro che destro in x0 esiste un limite finito per x che tende a x0.
$$ \lim_{x \rightarrow x_0} f(x) = l' $$
E così via.
