Intervallo in matematica

Un intervallo è un insieme di numeri/punti compresi tra due numeri a e b detti estremi dell'intervallo con a<b.

Gli intervalli aperti e chiusi

L'intervallo può essere

• chiuso [a,b] se gli estremi appartengono all'intervallo $$ [a,b] = \{ x \in R: a \le x \le b \} $$
  
• aperto (a,b) se gli estremi non appartengono all'intervallo
  $$ (a,b) = \{ x \in R: a < x < b \} $$
  

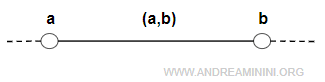
Nota. I numeri a e b sono detti estremi sia nell'intervallo chiuso che nell'intervallo aperto.

L'intervallo può anche essere

• aperto a sinistra e chiuso a destra (a,b] se l'estremo b appartiene all'intervallo mentre l'estremo a no $$ (a,b] = \{ x \in R: a < x \le b \} $$
  
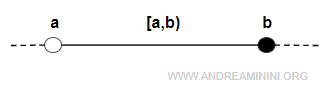
• chiuso a sinistra e aperto a destra [a,b) se l'estremo a appartiene all'intervallo mentre l'estremo b no
  $$ (a,b] = \{ x \in R: a \le x < b \} $$
  

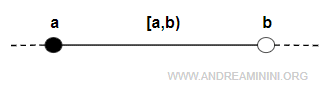
Gli intervalli limitati e illimitati

Un intervallo può essere limitato o illimitato

• intervallo limitato se gli estremi a e b dell'intervallo sono numeri finiti. $$ (a,b) $$
• intervallo illimitato se almeno uno dei due estremi è ±∞. $$ (a,+∞) \\ (-∞, b) \\ (-∞,+∞) = R $$
  

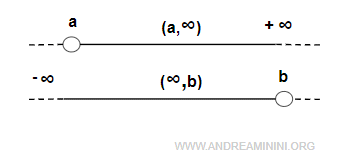
Nota. Negli intervalli illimitati l'infinito è sempre un estremo aperto perché l'infinito è soltanto un simbolo matematico che indica un insieme infinito di numeri. Pertanto, a seconda dei casi, un intervallo illimitato non ha un estremo superiore e/o inferiore. Ad esempio (a,+∞) e (-∞,b).Viceversa, l'estremo finito dell'intervallo illimitato può essere chiuso [a,+∞) e (-∞,b] o aperto (a,+∞) e (-∞,b).

E così via