ll limite della funzione
- Il limite (l) della funzione f(x) che tende a x0 $$ \lim_{x \rightarrow x_0} f(x) = l $$ può essere
- convergente se l è un numero finito
- divergente se l è infinito
- non esistente se la funzione è oscillante o il limite non esiste in x0
Dove x0 è un punto di accumulazione del dominio della funzione f(x), mentre l è un numero reale qualsiasi finito o infinito.
Il limite convergente
A] Se x0 è un numero finito
Il limite di una funzione f(x) per x che tende a x0 di R è uguale a l $$ \lim_{x \rightarrow x_0} f(x) = l $$ se e soltanto se preso un qualsiasi ε>0 esiste un numero δ>0 tale che $$ l-ε <f(x) < l+ε $$ per ogni x dell'intorno x0-δ<x<x0+δ.

Dove l è un numero reale finito.
In simboli
$$ \lim_{x \rightarrow x_0} f(x) = l \Leftrightarrow \forall \ ε>0 \, \ \exists \ δ>0: |f(x)-l|<ε, \forall \ x \in I:0 \ne |x-x_0|<δ $$
In altre parole, la funzione ha un limite reale $ l $ per $ x $ che tende a $ x_0 $, quando comunque si scelga un numero reale positivo $ \epsilon $, esiste un intorno completo $ I $ di $ x_0 $ tale che $ | f(x)-l | < \epsilon $ per ogni $ x $ appartenente a $ I $ diverso da $ x_0 $
Il punto $ x_0 $ è un punto di accumulazione, quindi può appartenere o meno all'intorno $ I $.
Quindi, una funzione $ f(x) $ può avere un limite reale finito $ l $ anche in un punto $ x_0 $ in cui non è definita.
Nota. Si può definire il limite di una funzione anche con le successioni estratte. Il limite di una funzione f(x) per x→x0 converge al numero finito $ l $ in un intorno $ I-\{ x_0 \} $ se qualsiasi successione estratta xn nell'intorno $ I $ con xn che tende a x0 risulta $ f(x_0)=l $.
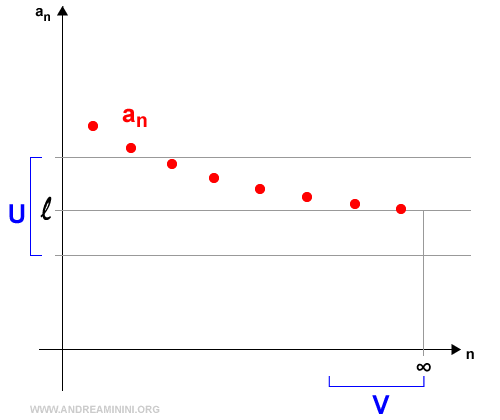
B] Se x0 è più o meno infinito
Il limite di una funzione f(x) per x che tende a infinito è uguale al limite finito l $$ \lim_{x \rightarrow ∞} f(x) = l $$ se e soltanto se preso un qualsiasi ε>0 esiste un numero k>0 tale che $$ |f(x)-l|< ε $$ per ogni x>k.
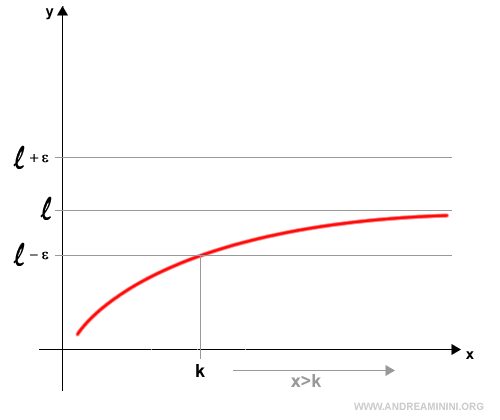
Dove l è un numero reale finito.
In simboli
$$ \lim_{x \rightarrow ∞} f(x) = l \Leftrightarrow \forall ε>0, \exists k>0: |f(x)-l|<ε, \forall x>k $$
La definizione per x che tende a -∞ è simile.
Esempio. Data la funzione f(x)=1/x) calcolo il limite per x→∞. $$ \lim_{x \rightarrow +∞} \frac{1}{x} = 0 $$
Il limite divergente a infinito
A] Se x0 è un numero finito
Il limite della funzione per x→x0 diverge a più infinito $$ \lim_{x \rightarrow x_0} f(x) = +∞ $$ se per ogni numero reale M>0 esiste un numero δ>0 tale che la funzione f(x) è maggiore di M per ogni x appartenente all'intorno x0-δ<x<x0+δ.

In simboli $$ \lim_{x \rightarrow x_0} f(x) = ∞ \Leftrightarrow \forall M>0, \exists δ>0: f(x)>M, \forall x \in A:0 \ne |x-x_0|<δ $$ In altre parole, preso un intorno sufficientemente piccolo di $ x_0 $, i valori della funzione $ f(x) $ diventano maggiori di qualsiasi numero positivo prefissato.
Il limite può essere più infinito (+∞) o meno infinito (-∞).
La funzione f(x) diverge a meno infinito $$ \lim_{x \rightarrow x_0} f(x) = -∞ $$ se per ogni numero reale M>0 esiste un numero δ>0 tale che la funzione f(x) è minore di -M per ogni x appartenente all'intorno x0-δ<x<x0+δ.
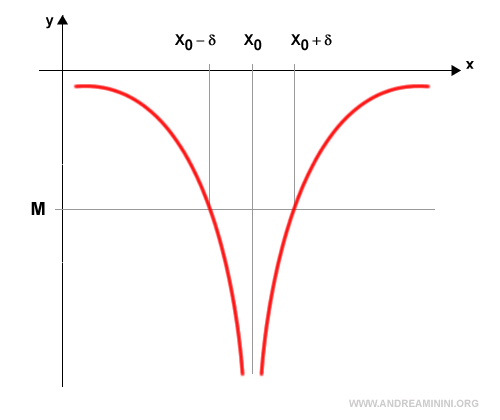
In simboli
$$ \lim_{x \rightarrow x_0} f(x) = -∞ \Leftrightarrow \forall M>0, \exists δ>0: f(x)<-M, \forall x \in A:0 \ne |x-x_0|<δ $$
In altre parole, preso un intorno sufficientemente piccolo di $ x_0 $, i valori della funzione $ f(x) $ diventano minori di qualsiasi numero negativo prefissato.
Esempio. Data la funzione f(x)=1/((x-1)^2) calcolo il limite per x→1. $$ \lim_{x \rightarrow 1} \frac{1}{(x-1)^2} = +∞ $$
B] Se x0 è più o meno infinito
Il limite della funzione per x→+∞ diverge a più infinito $$ \lim_{x \rightarrow +∞} f(x) = +∞ $$ se per ogni numero reale M>0 esiste un numero k>0 tale che f(x)>M per ogni x>k.

In simboli $$ \lim_{x \rightarrow +∞} f(x) = +∞ \Leftrightarrow \forall M>0, \exists k>0: f(x)>M, \forall x>k $$ In altre parole, facendo crescere $ x $, la funzione sale al di sopra di qualunque soglia positiva prefissata e continua a salire senza alcun limite superiore.
Il limite può essere più infinito (+∞) o meno infinito (-∞).
Il limite della funzione per x→+∞ diverge a meno infinito $$ \lim_{x \rightarrow +∞} f(x) = -∞ $$ se per ogni numero reale M>0 esiste un numero k>0 tale che f(x)<-M per ogni x>k.
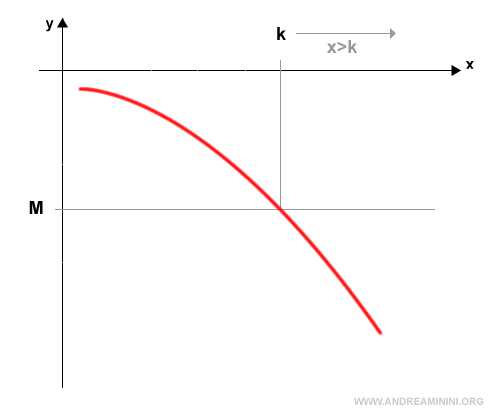
In simboli $$ \lim_{x \rightarrow +∞} f(x) = -∞ \Leftrightarrow \forall M>0, \exists k>0: f(x)<-M, \forall x>k $$
In altre parole, facendo crescere $ x $ senza limite, la funzione scende al di sotto di qualunque soglia negativa prefissata e continua a diminuire senza limite inferiore.
Esempio. Data la funzione f(x)=x2 calcolo il limite per x→∞. $$ \lim_{x \rightarrow +∞} x^2 = ∞ $$
In questi esempi ho mostrato il caso della x che tende a infinito. La definizione del limite per x→-∞ è simile.
Il limite non esistente
A] Se x0 è un numero finito
Il limite di una funzione per x che tende a x0 non esiste se il limite destro e il limite sinistro non coincidono. $$ \lim_{ x \rightarrow x_0^+ } f(x) \ne lim_{ x \rightarrow x_0^- } f(x) $$

In tali circostanze la funzione potrebbe essere non essere definita o avere un asintoto in x0.
B] Se x0 è più o meno infinito
Il limite di una funzione per x che tende a ±∞ non esiste se la funzione è oscillante o non è definita. $$ \lim_{ x \rightarrow ±∞ } f(x) = \: non \: esiste $$

Esempi
Prendo in considerazione la funzione
$$ f(x) = \frac{1}{x} $$
Il limite della funzione per x→0 non esiste
$$ \lim_{ x \rightarrow 0 } \frac{1}{x} = \: non \: esiste $$
Perché il limite destro è +∞
$$ \lim_{ x \rightarrow 0^+ } \frac{1}{x} = +∞ $$
mentre il limite sinistro è -∞
$$ \lim_{ x \rightarrow 0^- } \frac{1}{x} = -∞ $$
La funzione 1/x non è definita in x0=0 dove ha un asintoto verticale.
E così via.
