Teorema del rapporto delle successioni

Data una successione a_n con termini positivi, se la successione b_n=a_n+1/a_n converge a un limite l_b<1 allora la successione a_n tende a zero.

Un esempio pratico

Esempio 1

Prendo come esempio la successione

$$ a_n = \frac{n^2+1}{2^n} $$

La successione ha i termini positivi per n>0.

Definisco la successione del rapporto b_n

$$ b_n = \frac{a_{n+1}}{a_n} = \frac{ \frac{(n+1)^2+1}{2^{n+1}} } { \frac{n^2+1}{2^n} } = \frac{(n+1)^2+1}{2^{n+1}} \cdot \frac{2^n}{n^2+1} $$

$$ b_n = \frac{n^2+2n+1}{2 \cdot 2^n} \cdot \frac{2^n}{n^2+1 }= \frac{n^2+2n+1}{2n^2+2 } $$

Il limite per n→∞ della successione del rapporto b_n tende a 1/2 ossia a un valore inferiore a 1, perché si tratta di una frazione fratta tra due polinomi di grado due.

Quindi, nel computo del limite considero solo i termini di grado maggiore n²/2n² = 1/2

$$ \lim_{ n \rightarrow ∞} b_n = \lim_{ n \rightarrow ∞} \frac{n^2+2n+1}{2n^2+2 } =\lim_{ n \rightarrow ∞} \frac{n^2}{2n^2} = \frac{1}{2} < 1 $$

Pertanto, secondo il teorema del rapporto il limite per n→∞ della successione a_n tende a 0, ossia a_n è una successione infinitesima.

$$ \lim_{ n \rightarrow ∞ } a_n = \lim_{ n \rightarrow ∞ } \frac{n^2+1}{2^n} = 0 $$

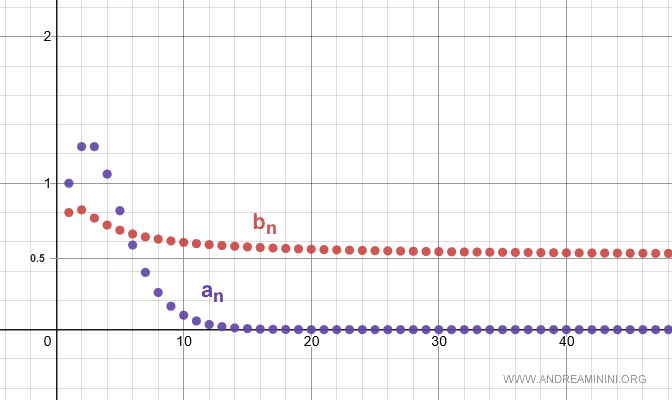
Ecco la rappresentazione grafica delle due successioni.

La dimostrazione

Ho una successione monotona a_n con termini positivi.

$$ a_n $$

Definisco una nuova successione composta dal rapporto tra i termini successivi della successione a_n.

$$ b_n = \frac{a_{n+1}}{a_n} $$

Per ipotesi il limite della successione b_n è minore di 1.

$$ \lim_{n \rightarrow ∞} b_n < 1 $$

Quindi, il limite della successione 1-b_n è maggiore di zero

$$ \lim_{n \rightarrow ∞} (1-b_n) > 0 $$

Per il teorema della permanenza del segno rispetto alla successione (1-b_n) esiste un indice v per cui b_n<1 per ogni n>v.

$$ b_n = \frac{a_{n+1}}{a_n} < 1 $$

ossia

$$ a_{n+1} < a_n $$

Questo vuol dire che la successione a_n è decrescente.

Nota. Soltanto se b_n<1 il limite della successione (1-b_n) può diventare maggiore di zero.

Inoltre, per l'ipotesi iniziale, la successione a_n è monotòna e ha tutti i termini positivi.

Essendo decrescente, monotona e con i termini positivi... la successione è anche una successione limitata perché il limite non può essere inferiore a zero.

Pertanto, secondo il teorema delle successioni monotone e limitate esiste un limite finito.

Questo limite è non negativo perché la successione ha tutti i termini positivi.

$$ \lim_{n \rightarrow ∞} a_n = l_a \ge 0 $$

Ricapitolando, il limite l_a è finito e non negativo.

Ci sono due soltanto risultati possibili:

• Il limite l_a è maggiore di zero
• Il limite l_a è uguale a zero

Se per assurdo il limite fosse maggiore di zero (l_a>0)

$$ \lim_{n \rightarrow ∞} a_n = l_a > 0 $$

Il limite della successione b_n diventerebbe pari a 1.

$$ \lim_{n \rightarrow ∞} b_n = \lim_{n \rightarrow ∞} \frac{a_{n+1}}{a_n} = \frac{ \lim_{n \rightarrow ∞} a_{n+1} }{ \lim_{n \rightarrow ∞} a_n } = \frac{l_a}{l_a} = 1 $$

Questo risultato è però impossibile, perché la successione b_n deve essere inferiore a 1.

$$ b_n = \frac{a_{n+1}}{a_n} < 1 $$

Quindi, per esclusione il limite (l_a) è uguale a zero.

$$ \lim_{n \rightarrow ∞} a_n = l_a = 0 $$

E questo dimostra il teorema.

E così via.