Limiti
Cos'è il limite
Il limite è uno strumento della matematica per studiare l'andamento di una funzione o di una successione quando il suo argomento x (nel caso delle funzioni) o l'indice (nel caso delle successioni) tende a un certo valore x0 finito o infinito. $$ \lim_{x \rightarrow x_0 } $$
Il limite di una successione
Il limite di una successione an descrive l'andamento della successione al crescere dell'indice n.
$$ \lim_{n \rightarrow x_0 } a_n = l $$
Dove x0 può essere un numero reale finito, più o meno infinito.
Il limite di una funzione
Il limite di una funzione f(x) descrive l'andamento della funzione quando l'argomento x tende a un determinato valore x0.
$$ \lim_{x \rightarrow x_0 } f(x) = l $$
Dove x0 può essere un numero reale finito, più o meno infinito.
La definizione generale di limite
La definizione di limite può essere generalizzata sia per le successioni che per le funzioni, poiché una successione è una particolare funzione f:N→R.
Inoltre, da una funzione f(x) è sempre possibile estrarre una successione di termini an=f(n) con n∈N.
Data una funzione f(x) definita nell'insieme I di R e un punto di accumulazione x0∈(-∞,+∞) per I, la funzione f(x) ha un limite uguale a l∈(-∞,+∞) per x che tende a x0 se per ogni intorno U di l esiste un intorno V di x0 tale che $$ x \in V-\{x_0\} \Rightarrow f(x) ∈ U $$
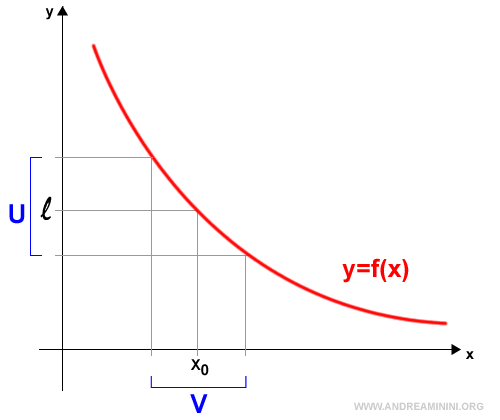
Poiché l'insieme dei numeri naturali N ha un solo punto di accumulazione pari a più infinito, nel caso delle successioni si calcola la successione soltanto per n→∞.
$$ \lim_{n \rightarrow ∞} a_n = l $$
Ecco la rappresentazione grafica del limite di una successione an.
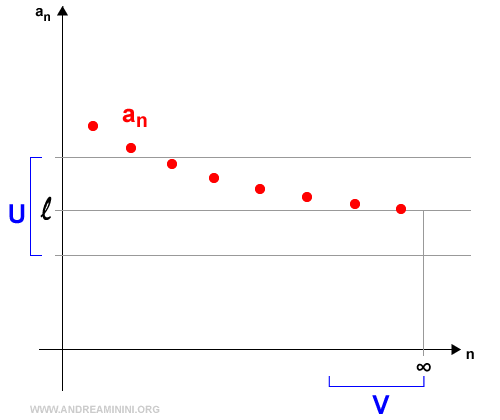
E così via.
