Limite di funzioni di 2 o più variabili

Prendo una funzione di due variabili f(x,y) $$ f:R^2 \rightarrow R $$ Il limite della funzione è$$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) $$che posso scrivere considerando la coppia di valori (x,y) come un vettore con due componenti $$ \lim_{\vec{x} \rightarrow \vec{x}_0} f( \vec{x} ) $$ dove $$ \vec{x} = (x,y) \\ \vec{x}_0 = (x_0,y_0) $$

Quando si parla di limite per una funzione di due variabili, come f(x,y), l'idea è simile a quella di una funzione di una variabile, ma con qualche complicazione in più.

A cosa serve il limite

Il limite indica il comportamento della funzione f(x,y) quando si avvicina al punto (x₀,y₀).

La funzione può avere uno dei seguenti comportamenti:

• convergere a un numero reale
  il limite è un numero reale finito che indica una quota sull'asse z.
• divergere a più o meno infinito
  il limite esiste ma è più o meno infinito. Ad esempo, se il limite è più infinito (+∞)  i valori di f(x,y) diventano arbitrariamente grandi quando (x,y) si avvicina a (x₀,y₀).
• non avere un limite
  il limite non esiste nel punto studiato. In questo caso la funzione non converge e non diverge.

Nota. Il concetto di limite è lo stesso già visto nelle funzioni di una variabile f(x). In questo caso, però le variabili indipendenti sono due (x,y) e indicano un punto del piano. L'intorno del punto (x₀,y₀) non è più l'intorno di un punto su una retta ma un intorno sferico di raggio δ nello spazio.

Un limite di funzione in due variabili esiste in un punto \((x_0, y_0)\) solo se il valore del limite è lo stesso lungo qualsiasi traiettoria di avvicinamento a quel punto.

Questo vale sia per traiettorie rettilinee, come \(y = mx\), sia per traiettorie curvilinee, come \(y = x^2\) o \(x = \rho \cos\theta,\, y = \rho \sin\theta\).

Quindi, mi basta trovare due traiettorie con limiti diversi per concludere che il limite non esiste in un punto \((x_0, y_0)\).

Limite convergente a un numero l di R

Il limite di una funzione di due variabili \(f(x,y)\) è un valore finito \(l\) se, avvicinandosi con \((x,y)\) al punto \((x_0, y_0)\), i valori di \(f(x,y)\) si avvicinano sempre più a \(l\). $$ \lim_{(x, y) \to (x_0, y_0)} f(x, y) = l $$ Formalmente, per ogni \(\epsilon > 0\), esiste un raggio \(\delta > 0\) tale che, per tutti i punti \((x,y)\) sufficientemente vicini a \((x_0, y_0)\) ma diversi da questo si ha \(|f(x,y) - l| < \epsilon\). 

Il limite della funzione f(x,y) che tende al punto (x₀,y₀) esiste ed è un numero finito

$$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) = l \ \in \ R $$

se per ogni epsilon maggiore di zero ε>0 , dove epsilon è un numero reale molto piccolo, esiste un numero reale delta maggiore di zero δ>0 tale che la funzione f(x,y) assume valori compresi tra l-ε e l+ε

$$ \forall \varepsilon > 0 \ \exists \ \delta >0 \ : \  \forall \ (x,y) \in B_δ(x_0,y_0) - \{ (x_0,y_0) \} \ , \ l - ε \lt f(x,y) \lt l + ε $$

Dove \(B_\delta(x_0, y_0)\) è un disco aperto di raggio \(\delta\) centrato in \((x_0, y_0)\).

In alternativa posso anche usare il simbolo del valore assoluto

\[ \forall \varepsilon > 0\ \exists \ \delta > 0 \ :  \forall (x, y) \in B_\delta(x_0, y_0) \setminus \{(x_0, y_0)\} \ , \   |f(x, y) - l| < \varepsilon \]

Dal punto di vista grafico, in ogni intorno circolare di raggio \(\delta\) del punto \((x_0, y_0)\), la superficie rappresentata da \(f(x, y)\) assume valori compresi tra \(l - \varepsilon\) e \(l + \varepsilon\). 

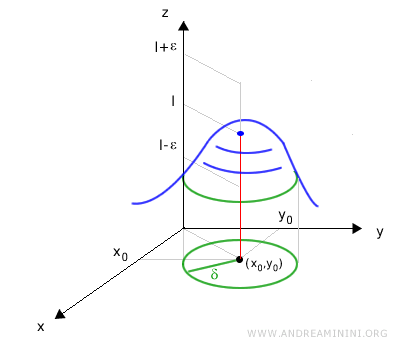
In altre parole, il grafico della funzione si appoggia sempre più vicino al piano \(z = l\) man mano che \((x, y)\) si avvicina a \((x_0, y_0)\).

Limite divergente a più infinito

Il limite di una funzione di due variabili \(f(x,y)\) è \(+\infty\) se, avvicinandosi con \((x,y)\) al punto \((x_0, y_0)\), i valori di \(f(x,y)\) crescono senza limite. Formalmente, questo significa che per ogni numero reale positivo \(M > 0\), esiste un raggio \(\delta > 0\) tale che, per tutti i punti \((x,y)\) sufficientemente vicini a \((x_0, y_0)\) ma diversi da esso, si ha \(f(x,y) > M\).

Il limite della funzione f(x,y) è più infinito nel punto (x₀,y₀)

$$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) = + \infty $$

se per qualsiasi numero reale M esiste un intorno sferico B di raggio δ del punto (x₀,y₀) in cui la funzione è sempre maggiore di M.

$$  \forall M > 0\ \exists \delta > 0 : \forall (x, y) \in B_\delta(x_0, y_0) \setminus \{(x_0, y_0)\},\ f(x, y) > M $$

Dal punto di vista grafico, l’intorno di raggio \(\delta\) è un disco aperto centrato nel punto \((x_0, y_0)\) sul piano \(xy\), mentre il numero reale \(M\) rappresenta una quota sull’asse \(z\). 

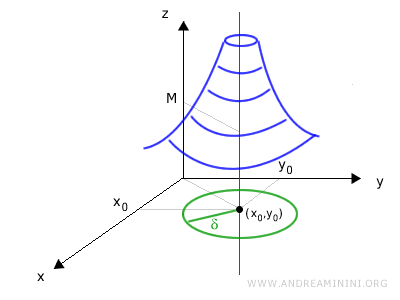
Dire che \(f(x, y) > M\) significa che il grafico della funzione si innalza verticalmente oltre qualunque livello assegnato, man mano che \((x, y)\) si avvicina a \((x_0, y_0)\).

Limite divergente a meno infinito

Il limite di una funzione di due variabili \(f(x,y)\) è \(-\infty\) se, avvicinandosi con \((x,y)\) al punto \((x_0, y_0)\), i valori di \(f(x,y)\) diminuiscono senza limite. Formalmente, questo significa che per ogni numero negativo \(M < 0\), esiste un raggio \(\delta > 0\) tale che, per tutti i punti \((x,y)\) sufficientemente vicini a \((x_0, y_0)\) ma diversi da \((x_0, y_0)\), si ha \(f(x,y) < M\).

Il limite della funzione f(x,y) è meno infinito

$$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) = - \infty $$

se per qualsiasi numero reale M esiste un intorno sferico B del punto (x₀,y₀) in cui la funzione è sempre minore di M.

$$  \forall M < 0\ \exists \delta > 0 : \forall (x, y) \in B_\delta(x_0, y_0) \setminus \{(x_0, y_0)\},\ f(x, y) < M $$

Dal punto di vista grafico, questo significa che, in ogni intorno sferico (disco aperto) \(B_\delta(x_0, y_0)\) centrato in \((x_0, y_0)\), i valori della funzione \(f(x, y)\) scendono sotto qualunque livello \(M\) fissato sull'asse \(z\).  

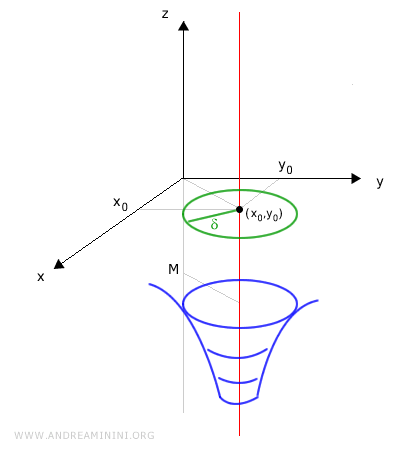
In altre parole, la superficie rappresentata da \(z = f(x, y)\) precipita verso il basso senza limite man mano che \((x, y)\) si avvicina a \((x_0, y_0)\).

Un esempio pratico

Devo studiare il limite della funzione f(x,y) per (x,y) che tende a (0,0)

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} $$

Si tratta di una forma indeterminata del tipo 0/0

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} = \frac{0}{0} $$

Provo a studiare il limito usando la tecnica del confronto.

La funzione è sicuramente non negativa per qualsiasi (x,y) perché tutte le incognite sono elevate ad esponente positivo pari.

Quindi posso scrivere la diseguaglianza

$$ 0 \le \frac{x^2 \cdot y^4}{x^2 + y^2} $$

D'altra parte la funzione è sicuramente inferiore o uguale a y⁴

$$ 0 \le \frac{x^2 \cdot y^4}{x^2 + y^2} \le y^4 $$

Spiegazione. L'espressione della funzione $$ \frac{x^2 \cdot y^4}{x^2 + y^2} $$ la posso scrivere in questa forma equivalente $$ y^4 \cdot \frac{x^2}{x^2 + y^2} $$ Il secondo fattore k=x²/(x²+y²) è un valore compreso tra 0 e 1 perché il denominatore è sempre maggiore o uguale al numeratore ( x² ≤ x²+y² ). Pertanto, il fattore y⁴ è moltiplicato per un valore k∈[0,1] compreso tra zero e uno. Quindi vale la diseguaglianza y⁴·k ≤ y⁴ ossia $$ y^4 \cdot \frac{x^2}{x^2 + y^2} \le y^4 $$

Calcolo il limite a tutti i membri della diseguaglianza

$$ \lim_{(x,y) \rightarrow (0,0)} 0 \le \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} \le \lim_{(x,y) \rightarrow (0,0)} y^4 $$

Il primo e l'ultimo limite sono pari a zero per (x,y) che tende a (0,0)

$$ 0 \le \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} \le 0 $$

Pertanto, per il teorema dei carabinieri anche il limite intermedio tende a 0.

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} = 0 $$

E così via.