La moltiplicazione tra matrici
La moltiplicazione di due matrici avviene calcolando il prodotto delle righe della prima matrice per le colonne della seconda matrice. Per questa ragione è detta moltiplicazione righe per colonne.

Data una matrice reale Amxn e una matrice reale Bnxp, il prodotto matriciale è una matrice reale Cmxp, i cui elementi cik sono la somma dei prodotti degli elementi corrispondenti della riga i di A e della colonna k di B.
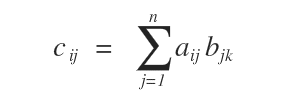
Questo tipo di prodotto tra matrici è possibile calcolarlo soltanto se la prima matrice ha un numero di colonne uguale al numero di righe della seconda matrice.
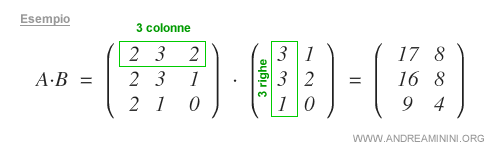
Nota. Spiegato in altri termini, il numero degli elementi contenuto in una riga della matrice A deve essere uguale al numero degli elementi contenuti in una colonna della matrice B.
Un esempio pratico
Voglio calcolare il prodotto delle matrici A e B.
La prima è una matrice 4x2 mentre la seconda è una matrice 2x4.
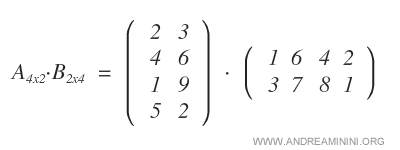
Il numero delle colonne di A è uguale al numero di righe di B. Quindi, posso procedere.
Nota. La matrice prodotto è una matrice ixk ossia 4x4 perché è ottenuta dalle quattro righe di A (i=4) per le quattro colonne di B (k=4).

Come primo passo moltiplico ogni riga della matrice A con la prima colonna della matrice B.
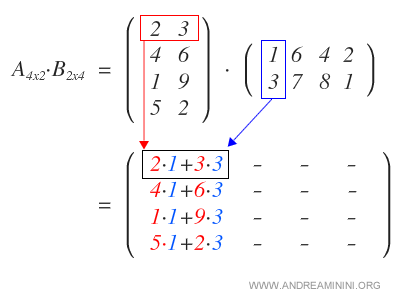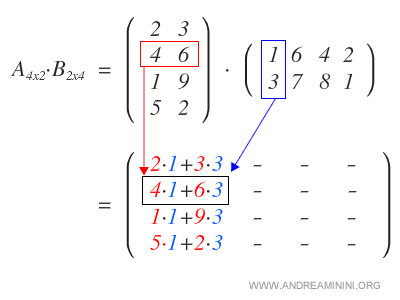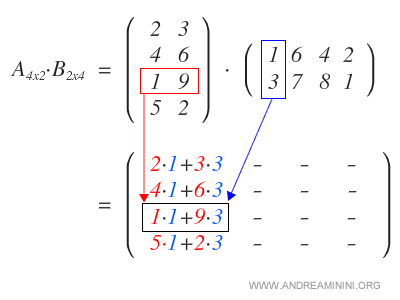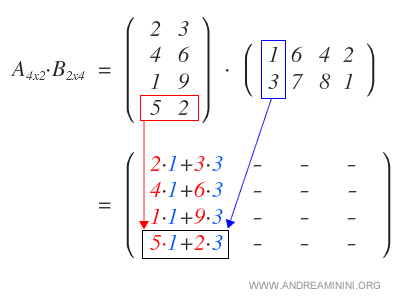
In questo modo ottengo la prima colonna della matrice prodotto.
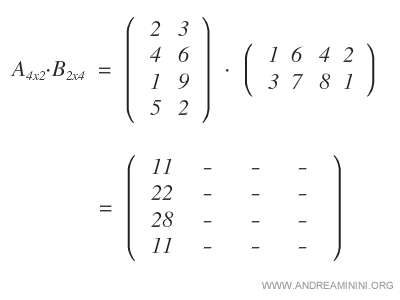
Poi moltiplico le righe di A per la seconda colonna di B.

Così facendo ottengo la seconda colonna della matrice prodotto.
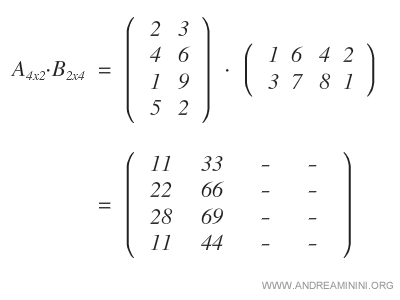
Poi moltiplico le righe di A per la terza colonna di B.

In questo modo calcolo la terza colonna della matrice prodotto.
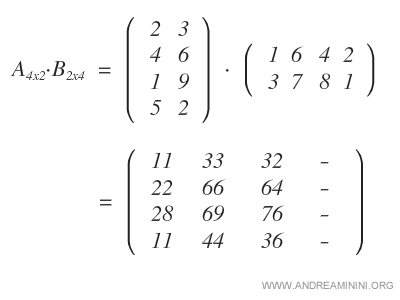
Infine, moltiplico le righe di A per la quarta colonna della matrice B.

In questo modo ottengo la quarta e ultima colonna della matrice prodotto.
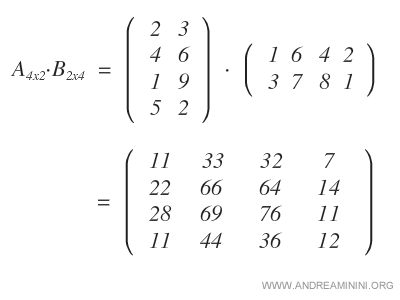
Ho così calcolato la matrice del prodotto A·B.
Le proprietà del prodotto tra matrici
La moltiplicazione tra matrici gode delle seguenti proprietà:
- Associatività. Date tre matrici A∈Mmn , B∈Mnp e C∈Mpq, il prodotto tra matrici A(BC) è uguale al prodotto (AB)C.
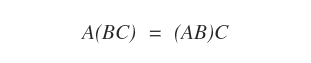
- Distributività a destra rispetto alla somma. Date tre matrici A∈Mmn , B∈Mnp e C∈Mnp, il prodotto tra matrici A(B+C) è uguale alla somma dei prodotti AB+AC.
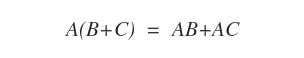
- Distributività a sinistra rispetto alla somma. Date tre matrici A∈Mmn , B∈Mnp e C∈Mnp, il prodotto tra matrici (A+B)C è uguale alla somma dei prodotti AC+BC.
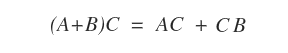
- Prodotto scalare. Date due matrici A∈Mmn , B∈Mnp e un numero reale qualsiasi α∈R, il prodotto α(AB) è uguale a (αA)B e A(αB).
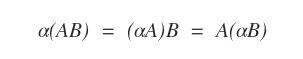
- Prodotto delle trasposte. Date due matrici A∈Mmn e B∈Mnp, la trasposta del prodotto delle matrici (AB)T è uguale al prodotto delle matrici trasposte BTAT.
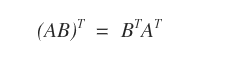
Nota. Nel prodotto delle matrici trasposte l'ordine dei fattori è invertito. Nel primo caso la prima matrice del prodotto è A mentre nel secondo caso è la matrice B.
Le differenze tra le matrici e i numeri reali
Il prodotto tra matrici non è commutativo
Il prodotto tra matrici non gode della proprietà commutativa.
La moltiplicazione A·B non dà lo stesso risultato di B·A.
Il prodotto non è commutativo perché invertendo l'ordine delle matrici si ottengono matrici di dimensioni diverse.
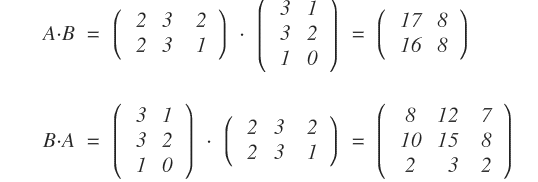
Nota. Ciò non esclude che ci siano anche casi in cui il prodotto AB sia uguale a BA. Ad esempio, se una delle due matrici è una matrice identità allora il prodotto gode della proprietà commutativa Tuttavia, si tratta di casi particolari e non di una regola generale.
Inoltre, in alcuni casi non è nemmeno possibile calcolare il prodotto commutativo.
Ad esempio, una matrice A potrebbe avere un numero di colonne uguale alle righe della matrice B ma diverso numero di righe rispetto alle colonne di B.

In questo caso il prodotto A·B è definito mentre il prodotto B·A non è definito.
Non vale la regola di annullamento del prodotto delle matrici
Nella moltiplicazione tra matrici non vale la regola di annullamento del prodotto.
Il prodotto tra una matrice A e una matrice nulla B dà sempre come risultato una matrice prodotto nulla.
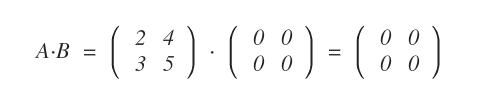
Tuttavia, la matrice nulla potrebbe essere ottenuta anche dal prodotto di due matrici non nulle.
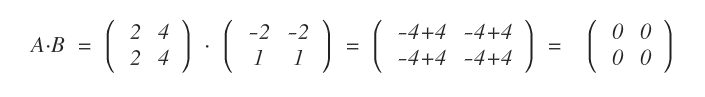
Per questa ragione, nella moltiplicazione tra matrici non vale la regola di annullamento del prodotto.
Le matrici non hanno un inverso moltiplicativo
Ogni numero reale ha un reciproco 1/x, tale che la moltiplicazione x·1/x è uguale a uno.
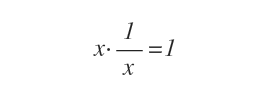
Le matrici, invece, non hanno questa proprietà. Non tutte le matrici hanno una matrice inversa.
Nota. Soltanto alcune matrici A, dette matrici invertibili, hanno una matrice inversa A-1 tale che A*A-1 è uguale a una matrice identità I.
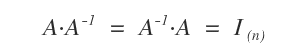
Come calcolare il prodotto riga per colonna tra matrici online
Questo strumento online permette di calcolare la moltiplicazione riga per colonna tra matrici quadrate o rettangolari e tra vettori.
