Il determinante della matrice

In algebra lineare il determinante della matrice è un numero che descrive le proprietà algebriche e geometriche di una matrice quadrata. Il determinante è indicato con le notazioni det(A) o |A|.

Esempio

Se la matrice quadrata è

$$ A= \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$

Allora il suo determinante posso indicarlo con det(A)

$$ det(A) = -2 $$

oppure con due barre verticali

$$ | A | = \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = -2 $$

Nota. Il determinante può essere calcolato soltanto nelle matrici quadrate, ossia nelle matrici che hanno un eguale numero di righe e colonne (m=n).

Come calcolare il determinante della matrice

Per il calcolo del determinante della matrice si possono usare diversi metodi.

Matrici quadrate di ordine 1

Nelle matrici quadrate di ordine 1, quelle composte da un solo elemento, il determinante della matrice è uguale al valore dell'elemento a₁₁.

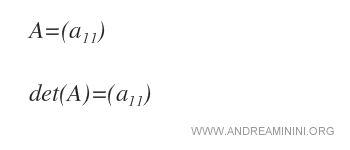
Esempio. Una matrice A di ordine 1 ha un solo elemento a₁₁=5. In questo caso il determinante det(A) è uguale a 5.

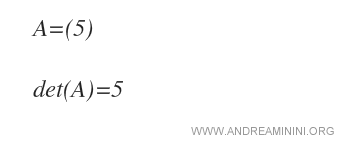
Matrici quadrate di ordine 2

Nelle matrici quadrate di ordine 2, il determinante è uguale al prodotto degli elementi della diagonale principale ( a₁₁·a₂₂) meno il prodotto degli elementi nella diagonale secondaria ( a₂₁·a₁₂).

Esempio. La seguente matrice A di ordine 2 è composta da due righe e due colonne. Il determinante det(A) è uguale a -2.

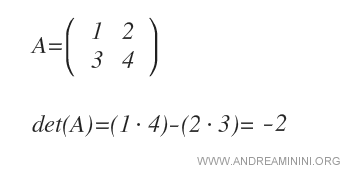
La regola di Sarrus

La regola di Sarrus calcola il determinante nelle matrici quadrate di ordine 3, quelle con tre righe e tre colonne (m=n=3).

Data una matrice di ordine 3.

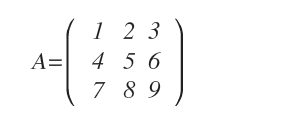
si affiancano sulla destra le prime due colonne

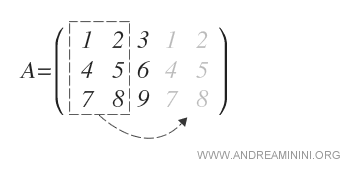
Quindi si sommano i prodotti delle diagonali che vanno da in alto a sinistra a in basso a destra

Poi si sottraggono i prodotti delle diagonali che vanno da in basso a sinistra a in alto destra.

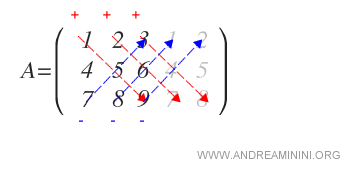
La somma algebrica dei prodotti è il determinante della matrice.

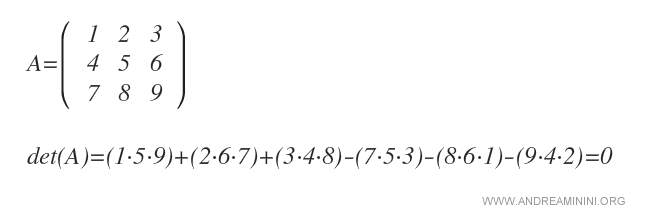
La regola di Sarrus in sintesi

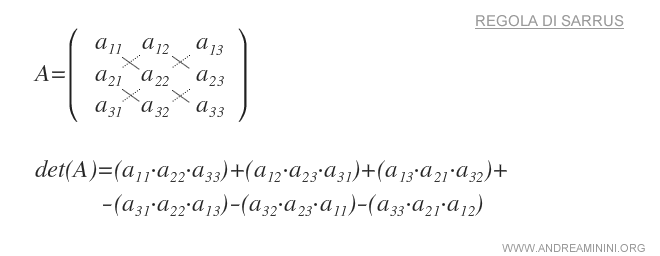
Lo sviluppo di Laplace

Uno dei metodi generali più usati nel calcolo del determinante è lo sviluppo di Laplace.

E' un algoritmo che mi permette di suddividere il calcolo del determinante usando matrici più piccole.

Prende il nome dal matematico francese Pierre-Simon Laplace.

Come funziona lo sviluppo di Laplace

Lo sviluppo di Laplace trasforma il calcolo di un determinante di ordine n al calcolo di n determinanti di ordine n-1.

1. Si sceglie una colonna j arbitraria della matrice.

   Quale colonna scegliere? Qualsiasi colonna della matrice va bene. E' però preferibile scegliere quella con più zeri, in questo modo si riducono i passaggi algebrici necessari per calcolare il determinante.

2. Una volta fissata la colonna j, si sommano i determinanti delle sottomatrici minori A_(ij) ottenute togliendo la riga i e la colonna j dalla matrice A secondo la seguente formula.
   

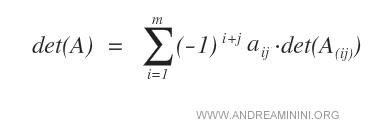
Esempio. Per calcolare il determinante della seguente matrice A di ordine 3 con lo sviluppo di Laplace, fisso la colonna j=1 e calcolo la sommatoria algebrica dei determinanti dei minori. Il determinante det(A) è uguale a zero.

Lo sviluppo di Laplace per riga

Lo sviluppo di Laplace funziona anche selezionando una riga della matrice anziché una colonna.

La formula è leggermente diversa perché in questo caso bisogna far scorrere le colonne j da 1 a n.

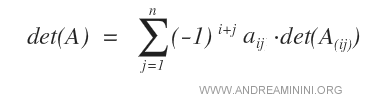
Il risultato finale è sempre lo stesso.

Esempio. In questo caso scelgo la prima riga. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot \begin{vmatrix} 1 & 2 & 3 \\ 0 & 5 & 1 \\ 0 & 0 & 2 \end{vmatrix} - 3 \cdot \begin{vmatrix} 0 & 2 & 3 \\ 0 & 5 & 1 \\ 0 & 0 & 2 \end{vmatrix} + 5 \cdot \begin{vmatrix} 0 & 1 & 3 \\ 0 & 0 & 1 \\ 0 & 0 & 2 \end{vmatrix} - 1 \cdot \begin{vmatrix} 0 & 1 & 2 \\ 0 & 0 & 5 \\ 0 & 0 & 0 \end{vmatrix} $$ Poi calcolo i determinanti delle quattro sottomatrici. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot 10 - 3 \cdot 0 + 5 \cdot 0 - 1 \cdot 0$$ Moltiplico i determinanti delle sottomatrici per i coefficienti. Infine, calcolo la somma dei prodotti. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 20 $$ Il determinante della matrice è 20.

Un consiglio per ridurre i calcoli. Quando uso questo metodo mi conviene scegliere la riga o la colonna con più zeri, perché in questo modo si semplificano i calcoli. Ad esempio, in questo caso scelgo la quarta riga. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = - 0 \cdot A_{(4,1)} + 0 \cdot A_{(4,2)} - 0 \cdot A_{(4,3)} + 2 \cdot \begin{vmatrix} 2 & 3 & 5 \\ 0 & 1 & 2 \\ 0 & 0 & 5 \end{vmatrix} $$ Molti coefficienti sono nulli e posso evitare di calcolare tre determinanti. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot \begin{vmatrix} 2 & 3 & 5 \\ 0 & 1 & 2 \\ 0 & 0 & 5 \end{vmatrix} $$ Poi reitero il procedimento scegliendo la terza riga della sottomatrice. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot \begin{vmatrix} 2 & 3 & 5 \\ 0 & 1 & 2 \\ 0 & 0 & 5 \end{vmatrix} = 2 \cdot 5 \cdot \begin{vmatrix} 2 & 3 \\ 0 & 1 \end{vmatrix} = 2 \cdot 5 \cdot (2 \cdot 1) = 20 $$ In questo modo riduco il calcolo del determinante di una matrice 4x4 in una matrice 2x2. Va comunque detto che in questo caso il calcolo potrebbe essere ancora più semplice. Essendo il determinante di una matrice triangolare, per ottenerlo basta moltiplicare gli elementi sulla diagonale principale. $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot 1 \cdot 5 \cdot 2 = 20 $$

I limiti dello sviluppo di Laplace. Il calcolo del determinante di una matrice con lo sviluppo di Laplace è poco efficiente nelle matrici quadrate di ordine elevato. Se la matrice quadrata è molto grande, è consigliabile utilizzare altri metodi più efficienti come il metodo di eliminazione di Gauss.

Il metodo di eliminazione di Gauss

Il determinante di una matrice quadrata può essere calcolato anche con il metodo di eliminazione di Gauss.

Si possono utilizzare le mosse di Gauss per trasformare la matrice in una forma a scalini per renderla triangolare superiore.

Per calcolare il determinante non occorre trasformare i pivot uguali a 1, perché nelle matrici triangolari il determinante è uguale al prodotto degli elementi della diagonale principale.

Bisogna però fare attenzione ai cambi di segno.

Secondo le proprietà del determinante, quando si scambia la posizione di due righe della matrice (R_x⇔R_y) il determinante cambia segno (-1·det).

Inoltre, il prodotto di una riga per uno scalare (k·R_x) moltiplica il determinante per lo scalare (k·det).

Il segno del determinante, invece, non varia (det) quando si somma una riga con il multiplo di un'altra riga della matrice (R_x+k·R_y).

Esempio. Per calcolare il determinante della matrice A utilizzo il metodo di eliminazione di Gauss.

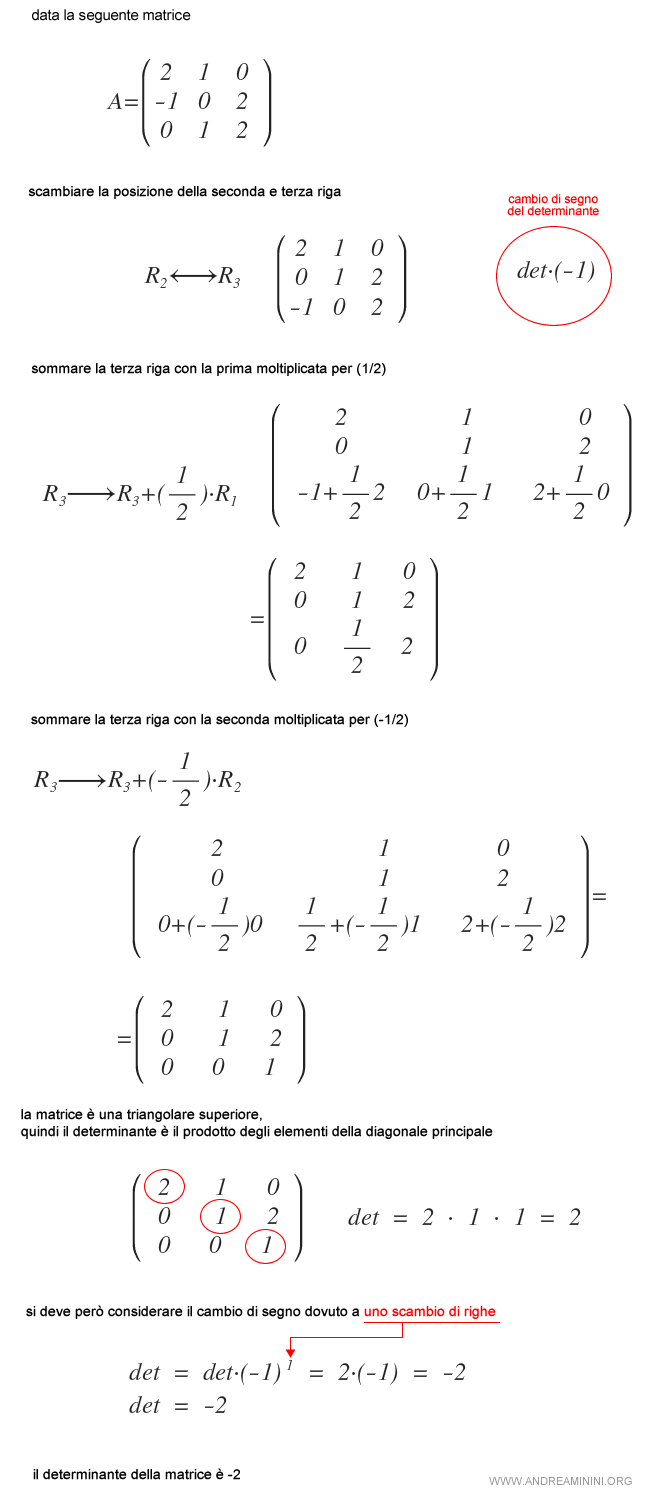
Quali sono i vantaggi del metodo di Gauss?

Quando le matrici sono molto grandi, il metodo di eliminazione di Gauss calcola il determinante molto più rapidamente rispetto allo sviluppo di Laplace.

Le proprietà del determinante

Alcune proprietà utili del determinante delle matrici quadrate

• Se la matrice quadrata ha almeno una riga o una colonna con tutti zeri, allora il determinante è nullo.

  Esempio. $$ \begin{vmatrix} 1 & 2 & 3 \\ 0 & 0 & 0 \\ 7 & 8 & 9 \end{vmatrix} = 0 $$ $$ \begin{vmatrix} 1 & 2 & 0 \\ 4 & 5 & 0 \\ 7 & 8 & 0 \end{vmatrix} = 0 $$

• Se la matrice quadrata è diagonale oppure triangolare superiore o inferiore, allora il determinante è uguale al prodotto degli elementi nella diagonale principale.

  Esempio. $$ \begin{vmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 0 & 0 & 9 \end{vmatrix} = 1 \begin{vmatrix} 5 & 6 \\ 0 & 9 \end{vmatrix} - 2 \begin{vmatrix} 0 & 6 \\ 0 & 9 \end{vmatrix} + 3 \begin{vmatrix} 0 & 5 \\ 0 & 0 \end{vmatrix} $$ $$ = 1 \cdot (5 \cdot 9 - 6 \cdot 0) - 2 \cdot (0 \cdot 9 - 6 \cdot 0) + 3 \cdot (0 \cdot 0 - 5 \cdot 0) $$ $$ = 1 \cdot 5 \cdot 9 $$

• Il determinante della matrice A è uguale al determinante della matrice trasposta A^T $$ det(A) = det(A^T) $$

  Esempio. $$ det(A) = \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = -2 $$ $$ det(A^T) = \begin{vmatrix} 1 & 3 \\ 2 & 4 \end{vmatrix} = -2 $$

• Se una matrice quadrata ha due righe uguali oppure due colonne uguali, allora il suo determinante è nullo.

  Esempio. Se la matrice ha due righe uguali $$ det(A) = \begin{vmatrix} a & b \\ a & b \end{vmatrix} = ab - ba = 0 $$ $$ det(A) = \begin{vmatrix} a & b & c \\ a & b & c \\ d & e & f \end{vmatrix} = d \begin{vmatrix} b & c \\ b & c \end{vmatrix} - e \begin{vmatrix} a & c \\ a & c \end{vmatrix} + f \begin{vmatrix} a & b \\ a & b \end{vmatrix} = d \cdot 0 - e \cdot 0 + f \cdot 0 = 0 $$ Se la matrice ha due colonne uguali, la sua trasposta ha due righe uguali. Quindi, il determinante è nullo. $$ det(A) = \begin{vmatrix} a & a \\ b & b \end{vmatrix} = det(A^T) = \begin{vmatrix} a & b \\ a & b \end{vmatrix} = 0 $$

• Se si scambiano due righe (o due colonne) fra loro in una matrice quadrata si ottiene il valore opposto del determinante.

  Esempio. Il determinante di questa matrice quadrata è -2 $$ \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = -2 $$ Scambio due righe fra loro $$ \begin{vmatrix} 3 & 4 \\ 1 & 2 \end{vmatrix} = 2 $$ Il risultato è il valore opposto del determinante.

• Teorema di Binet
  Date due matrici quadrate A e B di ordine n, il determinante del prodotto delle matrici è uguale al prodotto dei determinanti delle due matrici. $$ det(A \cdot B) = det(A) \cdot det(B) $$

  Esempio. Considero due matrici $$ A=\begin{pmatrix} 1 & 4 \\ 3 & 2 \end{pmatrix} $$ $$ B=\begin{pmatrix} 2 & 1 \\ 5 & 3 \end{pmatrix} $$ I determinanti delle due matrici sono $$ det(A) = -10 $$ $$ det(B) = 1 $$ Calcolo il prodotto delle due matrici che a sua volta è una matrice $$ A \cdot B =\begin{pmatrix} 1 & 4 \\ 3 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\ 5 & 3 \end{pmatrix} = \begin{pmatrix} 22 & 13 \\ 16 & 9 \end{pmatrix} $$ Il determinante della matrice prodotto è $$ \det(A \cdot B) = -10 $$ Se moltiplico i determinati delle matrici A e B ottengo lo stesso risultato, ossia il determinante della matrice prodotto. $$ \det(A) \cdot \det(B) = -10 \cdot 1 = -10 $$

• Data una matrice M di ordine n e un numero scalare k si ha $$ \det(k \cdot M) = k^n \cdot \det(M) $$

  Dimostrazione. Il prodotto di una matrice di ordine n=2 per uno scalare k è $$ k \cdot M = \begin{pmatrix} ka & kb \\ kc & kd \end{pmatrix} $$ Pertanto, il calcolo del determinante è $$ det(k \cdot M) = ka \cdot kd - kb \cdot kc = k^2ad-k^2bc =k^2 \cdot (ad-bc)=k^2 \cdot det(M) $$ Questa proprietà è utile per semplificare una matrice se tutti gli elementi possono essere raccolti a fattore comune.
  Esempio. In questa matrice tutti gli elementi sono divisibili per due $$ M = \begin{pmatrix} 6 & 8 \\ 4 & 2 \end{pmatrix} $$ Per calcolare il determinante divido tutti i membri per due e moltiplico il determinante per 2². $$ \det(M) = 2^2 \cdot det \begin{pmatrix} \frac{6}{2} & \frac{8}{2} \\ \frac{4}{2} & \frac{2}{2} \end{pmatrix} = 4 \cdot det \begin{pmatrix} 3 & 4 \\ 2 & 1 \end{pmatrix} = 4 \cdot (3 \cdot 1 - 4 \cdot 2) = -20 $$ Il calcolo del determinante è più semplice perché gli elementi della matrice sono più piccoli.

• Se una matrice quadrata M ha una riga che è multipla di un'altra riga, oppure una colonna che è multipla di un'altra colonna, allora il determinante è nullo.

  Esempio. Questa matrice ha una riga multipla dell'altra. $$ det \begin{pmatrix} 2 & 4 \\ 4 & 8 \end{pmatrix} = 2 \cdot 8 - 4 \cdot 4 = 16 - 16 = 0 $$ Il determinante è nullo.

Il determinante delle matrici triangolari

Il determinante di una matrice triangolare è uguale al prodotto degli elementi sulla diagonale principale.

Questo accade perché gli altri prodotti sono nulli.

Pertanto, se la matrice è triangolare il calcolo si semplifica notevolmente.

Esempio

Considero la matrice

$$ A = \begin{pmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{pmatrix} $$

Il determinante della matrice è uguale al prodotto degli elementi che si trovano sulla diagonale principale.

$$ det(A) = 2 \cdot 1 \cdot 5 \cdot 2 = 20 $$

Osservazioni

Alcune osservazioni finali sul determinante

• Il determinante è un invariante completo della trasposizione, perché una matrice quadrata M e la sua matrice trasposta M^T hanno lo stesso determinante $$ \det(M) = \det(M^T) $$

Il calcolo del determinante online

Questo strumento permette di calcolare online il determinante di una matrice quadrata.