Il limite per eccesso e il limite per difetto
Quando una funzione ammette un limite finito \( l \) per \( x \to x_0 \), posso precisare come la funzione si avvicina a quel valore. In particolare, può avvicinarsi dall’alto oppure dal basso. Questa distinzione porta ai concetti di limite per eccesso e limite per difetto.
Dal punto di vista pratico, guardando il grafico della funzione, si osserva che:
- nel limite per eccesso, il grafico della funzione si avvicina alla retta \( y = l \) dall’alto
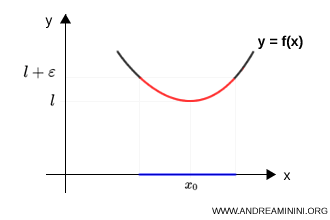
- nel limite per difetto, il grafico si avvicina alla stessa retta dal basso
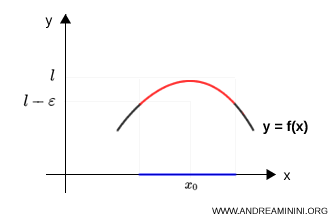
Il valore del limite è lo stesso, ma cambia il comportamento locale della funzione.
Nota. L’idea è semplice: non basta sapere a quale numero tende la funzione, ma anche da quale direzione lo raggiunge. Quindi, il limite per eccesso e per difetto non sono nuovi tipi di limite, ma solo una precisazione qualitativa del limite finito.
Il limite per eccesso
Si dice che una funzione \( f(x) \) tende al valore \( l \) per eccesso quando:
- il limite di \( f(x) \) per \( x \to x_0 \) è \( l \)
- in un intorno di \( x_0 \), escluso al più il punto \( x_0 \), la funzione assume solo valori maggiori di \( l \)
In simboli si scrive:
\[ \lim_{x \to x_0} f(x) = l^{+} \]
Dal punto di vista analitico, equivale a richiedere che per ogni \( \varepsilon > 0 \), scegliendo opportunamente un intorno di \( x_0 \), sia rispettata la condizione:
\[ l < f(x) < l + \varepsilon \]
Sottraendo $ l $ da ogni membro della disequazione ottengo:
\[ 0 < f(x) - l < \varepsilon \]
In altre parole, la funzione \( f(x) \) si avvicina a \( l \), ma rimane sempre sopra quel valore.

Ad esempio, se una funzione ha come limite \( l = 2 \) e per \( x \) che tende a \( x_0 \), assume valori come 2.1, 2.01, 2.001, ... senza mai raggiungere, né superare 2, allora la funzione si avvicina a 2 dall'alto e il limite è per eccesso.
Esempio
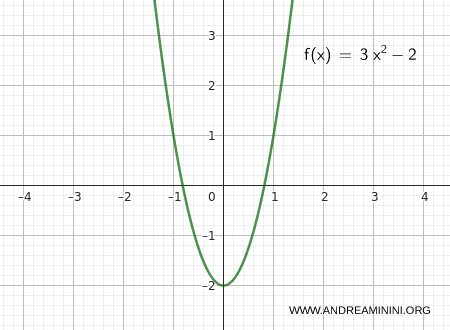
Considero la funzione:
\[ f(x) = 3x^2 - 2 \]
Voglio verificare che:
\[ \lim_{x \to 0} (3x^2 - 2) = -2^{+} \]
Fisso un numero \( \varepsilon > 0 \) e impongo la condizione:
\[ 0 < f(x) - l < \varepsilon \]
Sapendo che $ f(x) = 3x^2 - 2 $ e $ l=-2 $
\[ 0 < (3x^2 - 2) - (-2) < \varepsilon \]
\[ 0 < 3x^2 < \varepsilon \]
La prima disuguaglianza \( 0 < 3x^2 \) è sempre vera per \( x \neq 0 \), perché \( x^2 > 0 \).
La seconda diseguaglianza \( 3x^2 < \varepsilon \) mi permette di ricavare la variabile x:
\[ x^2 < \frac{\varepsilon}{3} \]
ossia
\[ -\frac{\sqrt{\varepsilon}}{3} < x < \frac{\sqrt{\varepsilon}}{3} \]
In questo intorno di \( 0 \), escluso il punto \( x=0 \), vale la condizione:
\[ -2 < f(x) < -2 + \varepsilon \]
Quindi, la funzione si avvicina a -2 dall’alto e il limite è per eccesso.
Il limite per difetto
Si dice che una funzione \( f(x) \) tende al valore \( l \) per difetto quando:
- il limite di \( f(x) \) per \( x \to x_0 \) è \( l \)
- in un intorno di \( x_0 \), con al più \( x \neq x_0 \), la funzione assume solo valori minori di \( l \)
In simboli:
\[ \lim_{x \to x_0} f(x) = l^{-} \]
Dal punto di vista analitico, la condizione si scrive come:
\[ l - \varepsilon < f(x) < l \]
Sottraendo $ l $ da ogni membro della diseguaglianza ottengo:
\[ - \varepsilon < f(x) - l < 0 \]
In questo caso, la funzione \( f(x) \) si avvicina a \( l \), ma rimane sempre sotto quel valore.

Ad esempio, se una funzione ha come limite \( l = 2 \) e, avvicinandosi a \( x_0 \), assume valori come 1.9, 1.99, 1.999, ... senza mai superare 2, allora il limite è per difetto.
Esempio
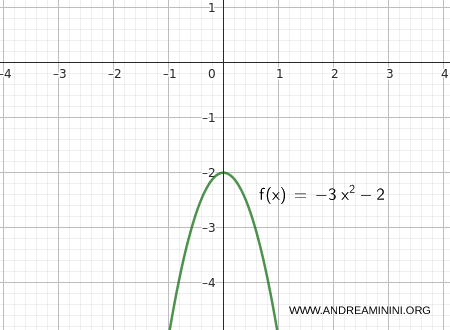
Considero la funzione:
\[ f(x) = -3x^2 - 2 \]
Voglio verificare che:
\[ \lim_{x \to 0} (-3x^2 - 2) = -2^{-} \]
Fisso un numero \( \varepsilon > 0 \) e impongo la condizione:
\[ -\varepsilon < f(x) - l < 0 \]
\[ -\varepsilon < (-3x^2 - 2) - (-2) < 0 \]
\[ -\varepsilon < -3x^2 < 0 \]
\[ -\varepsilon < -3x^2 < 0 \]
La seconda disuguaglianza \( -3x^2 < 0 \) è sempre vera per \( x \neq 0 \), perché \( x^2 > 0 \) e il coefficiente \( -3<0 \). Il prodotto tra un numero positivo e uno negativo è sempre negativo, ossia minore di zero.
La prima diseguaglianza \( -\varepsilon < -3x^2 \) mi permette di ricavare la variabile x:
Divido entrambi i membri della diseguaglianza per -3. Quando si divide una disequazione per un numero negativo, il verso si inverte.
\( \frac{-\varepsilon}{-3} > \frac{ -3x^2 }{-3} \]
\( \frac{\varepsilon}{3} > x^2 \]
ossia
\[ - \sqrt{ \frac{\varepsilon}{3} } < x < \sqrt{ \frac{\varepsilon}{3} } \]
In questo intorno di \( 0 \), escluso il punto \( x=0 \), vale la condizione:
\[ -2 - \varepsilon < f(x) < -2 \]
Quindi, la funzione f(x) si avvicina a -2 dal basso e il limite è per difetto.
E così via.
