Matrice triangolare superiore
Una matrice quadrata è detta matrice triangolare superiore se gli elementi sotto la diagonale principale sono nulli. $$ \forall \ i > j \ \ \ \ a_{ij } = 0 $$
Un esempio pratico
Ecco un esempio di matrice triangolare superiore di ordine 3, con tre righe e tre colonne.
Gli elementi sotto la diagonale principale sono tutti nulli.
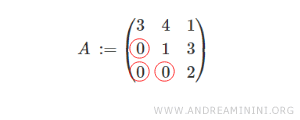
Nota. Non occorre che gli altri elementi della matrice siano diversi da zero. Possono anche essere nulli.
Se anche la diagonale principale è composta da elementi nulli, la matrice triangolare superiore è detta strettamente triangolare superiore.
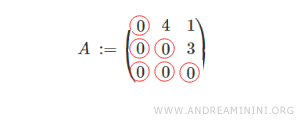
L'insieme delle matrici triangolari superiori a coefficienti reali R di ordine n si indica con il simbolo T con il tipo di numeri (R) in apice.
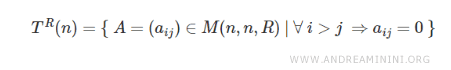
A cosa servono le matrici triangolari?
Le matrici triangolari sono particolarmente utili perché riducono la complessità computazionale dell'elaborazione, in quanto i dati sono concentrati in una sola parte della matrice.
Inoltre, il determinante di una matrice triangolare è uguale al prodotto degli elementi sulla diagonale principale perché tutti gli altri prodotti sono nulli.
E così via.
