Matrice triangolare inferiore
Una matrice quadrata è detta matrice triangolare inferiore se gli elementi sopra la diagonale principale sono nulli. $$ \forall \ i < j \ \ \ \ a_{ij } = 0 $$
Un esempio pratico
Ecco un esempio di matrice triangolare inferiore di ordine 3, con tre righe e tre colonne.
Tutti gli elementi sopra la diagonale principale sono nulli.
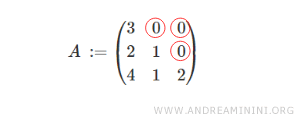
Nota. Non è necessario che gli altri elementi della matrice debbano essere diversi da zero. Possono anche essere nulli.
Se anche la diagonale principale è composta da elementi nulli, la matrice triangolare inferiore è detta strettamente triangolare inferiore.
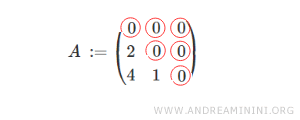
L'insieme delle matrici triangolari inferiori a coefficienti reali R di ordine n si indica con il simbolo T e il tipo di numeri (R) in pedice.
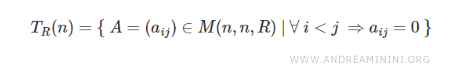
Nota. Le matrici triangolari riducono la complessità dei calcoli durante l'elaborazione perché i dati si trovano soltanto in una parte della matrice. Quindi, meno calcoli da svolgere e meno spazio di memoria in cui scrivere i dati.
A cosa serve una matrice triangolare inferiore?
Gli elementi di una matrice triangolare inferiore occupano solo metà dello spazio della matrice quadrata. Questo semplifica le operazioni computazionali.
Inoltre, il determinante di una matrice triangolare è uguale al prodotto degli elementi sulla diagonale principale perché tutti gli altri prodotti sono nulli.
E così via.
