Le rette parallele
Due rette sono rette parallele quando non hanno alcun punto in comune oppure coincidono.
Per indicare due rette parallele si usa il simbolo // oppure ||
$$ r // s $$ $$ r \parallel s $$
La regione del piano compresa tra le due rette è detta "striscia" oppure "banda".
La distanza minima di un qualsiasi punto di una retta dall'altra retta parallela è, invece, chiamata "altezza" della striscia o distanza tra le rette parallele.
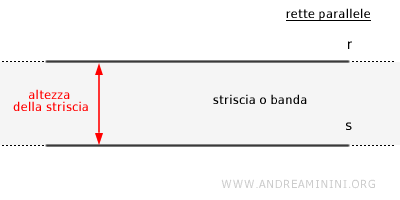
Questa altezza rappresenta la misura perpendicolare tra le due rette ed è costante in ogni punto di ciascuna retta.
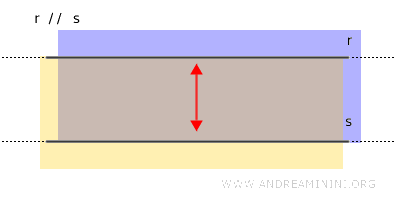
Nota. La striscia tra due rette parallele distinte $ r $ e $ s $può anche essere vista come l'intersezione tra il semipiano che ha origine da $ r $ e contiene $ s $ e il semipiano che ha origine da $ s $ e contiene $ r $.
- Il quinto postulato di Euclide
- La condizione necessaria e sufficiente per il parallelismo tra due rette
- Il teorema delle rette parallele (criterio di parallelismo)
- Una definizione alternativa
- La condizione di parallelismo delle rette
- Come capire se due rette sono parallele distinte o coincidenti
- Osservazioni
Il quinto postulato di Euclide
Per un punto $ P $ esterno a una retta $ r $ passa una sola retta parallela $ s || r $ .
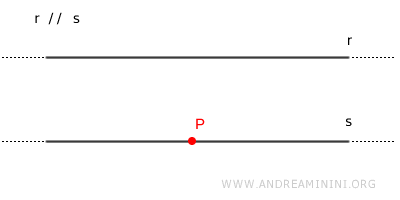
Il quinto postulato di Euclide è noto anche come postulato delle parallele.
E' il più famoso e controverso dei postulati euclidei, perchè è l’unico che non appare evidente o intuitivo come gli altri.
In particolar modo, si può dimostrare l'esistenza ma non si può dimostrare che per un punto $ P $ esterno a una retta $ r $, passa una sola retta parallela.
Cosa si può dedurre dal postulato?
Dal postulato derivano diverse proprietà geometriche delle rette parallele.
- Teorema della transitività delle rette parallele
Due rette a e b parallele a una terza retta c, sono anche parallele tra loro (a || b) $$ a \parallel c \ , \ b \parallel c \ \Rightarrow a \parallel b $$Dimostrazione. Per dimostrarlo seguo un ragionamento per assurdo. Per ipotesi le rette a e b sono entrambe parallele alla retta c ma le rette a e b non sono parallele tra loro $$ a \parallel c $$ $$ b \parallel c $$ Se le rette a e b non sono parallele, allora sono incidenti in un punto P.
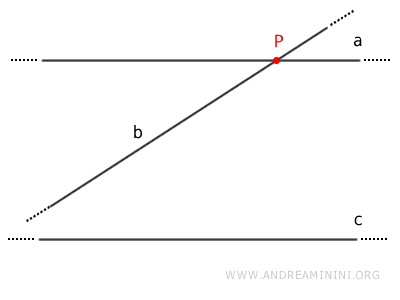
Tuttavia, per l'ipotesi iniziale entrambe le rette a e b sono parallele alla retta c. Questo vuol dire che nel punto P passano due rette (a e b) parallele alla retta c, ma questo è impossibile perché contraddice il postulato delle parallele (unicità). Pertanto le rette a e b non possono essere incidenti. Quindi, l'affermazione iniziale è falsa. E' vera la sua negazione ossia le rette a e b sono entrambe parallele alla retta c e sono anche parallele tra loro (a || b)
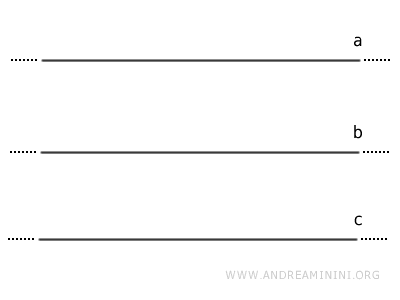
- Il parallelismo tra le rette è una relazione di equivalenza
L'insieme di tutte le rette parallele a una retta $r$ si chiama direzione. Questo insieme costituisce una classe di equivalenza, poiché ogni retta della classe è parallela alle altre e insieme formano un fascio improprio di rette. Di conseguenza, il parallelismo tra rette è una relazione di equivalenza, in quanto soddisfa le tre proprietà fondamentali: riflessività, simmetria e transitività.- Proprietà riflessiva
Una retta r è sempre parallela a se stessa. $$ r \parallel r $$Nota. Questa proprietà deriva dalla definizione stessa di retta parallela.
- Proprietà simmetrica
Se una retta r è parallela alla retta s, allora la retta s è parallela alla retta r. $$ r \parallel s $$Nota. Questa proprietà è una conseguenza della definizione di retta parallela.
- Proprietà transitiva
Se le rette r || s sono parallele e le rette s || p sono parallele, allora anche le rette r || p sono parallele. $$ r \parallel s \ , \ s \parallel p \ \Rightarrow r \parallel p $$Nota. Questa proprietà deriva dal fatto che due rette parallele a una terza retta, sono anche parallele tra loro (teorema di transitività delle rette parallele).
- Proprietà riflessiva
- Teorema delle rette incidenti con un fascio di rette parallele
Se una retta $ r $ è incidente a una retta $ a $ di un fascio improprio di rette $ a \parallel b \parallel c ... $, allora è incidente anche a tutte le altre rette del fascio $ r \parallel b \parallel c ...$
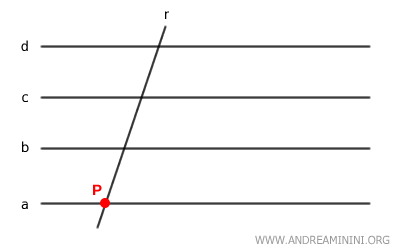
Dimostrazione. Come ipotesi iniziale considero un fascio improprio di rette parallele: $$ a \parallel b \parallel c \parallel ... $$ e una retta $ r $ che incontra la retta $ a $ in un punto $ P $: $$ r \cap a = \{ P \} $$ Devo dimostrare che la retta $ r $ è incidente anche con tutte le altre rette del fascio. Procedo per assurdo. Suppongo che $ r $ non sia incidente con una retta $ b $ del fascio: $$ r \cap b = \emptyset $$ Allora, per definizione, $ r $ e $ b $ sarebbero parallele: $$ r \parallel b $$ Ma poiché $ b \parallel a $, per la proprietà transitiva del parallelismo avrei anche: $$ r \parallel a $$ Questo però è in contraddizione con l'assioma delle rette parallele, perché per l'ipotesi iniziale $ r $ incontra $ a $ nel punto $ P $ e due rette parallele non possono avere punti in comune. Dunque la tesi $ r \cap b = \emptyset $ è falsa. Ne consegue che è vera la tesi contraria. $$ r \cap b \ne \emptyset $$ Lo stesso ragionamento posso ripeterlo per ogni altra retta del fascio. Pertanto, la retta $ r $ è incidente con tutte le rette del fascio.
La condizione necessaria e sufficiente per il parallelismo tra due rette
Per stabilire se due rette sono parallele, è necessario verificare due condizioni fondamentali:
Complanarità
Le due rette parallele devono essere complanari, ossia devono appartenere allo stesso piano.
Senza la complanarità, due rette non possono essere parallele.
Quindi, la complanarità è la condizione necessaria ma non sufficiente del parallismo.
Ad esempio, nello spazio tridimensionale quando le rette non sono complanari, allora sono dette sghembe e, per definizione, non possono essere parallele.
Non incidenza
Le due rette parallele devono essere complanari e non incidenti.
In altre parole, oltre a essere complanari, le due rette non devono essere incidenti, cioè non devono avere punti in comune.
Questa è la condizione necessaria e sufficiente del parallelismo delle rette.
Quando le due rette sono nello stesso piano e non si incontrano mai, allora sono sicuramente parallele.
Il teorema delle rette parallele (criterio di parallelismo)
Se due rette tagliate da una terza retta trasversale soddisfano una di queste condizioni
- formano angoli alterni (interni o esterni) congruenti
- formano angoli corrispondenti (interni o esterni) congruenti
- formano angoli coniugati supplementari (α+β=180°)
allora le due rette sono rette parallele.
Questo teorema è anche detto criterio di parallelismo delle rette.
Vale anche il teorema inverso, quindi se due rette sono parallele allora formano con una trasversale delle coppie di angoli alterni (interni o esterni) congruenti, angoli corrispondenti congruenti e angoli coniugati (interni o esterni) supplementari.
Una definizione alternativa
Due rette (non parallele all'asse y) sono parallele tra loro se hanno lo stesso coefficiente angolare e viceversa.
In pratica, due rette qualsiasi sono parallele se hanno la stessa pendenza rispetto all'asse delle ascisse (x).
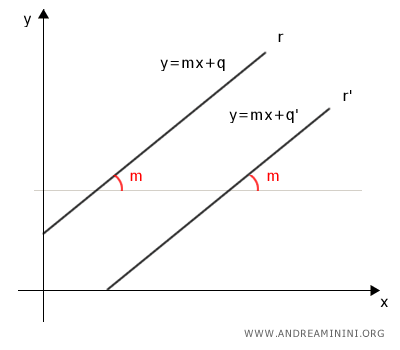
Fanno eccezione alla regola tutte le rette parallele all'asse delle ordinate (y) poiché, in questo caso, non è possibile determinare il coefficiente angolare.
Teorema inverso. Se due rette hanno lo stesso coefficiente angolare (m=m') allora sono rette parallele.
Un esempio pratico e dimostrazione
Considero due rette parallele r:y=2x-2 e r':y=2x-6
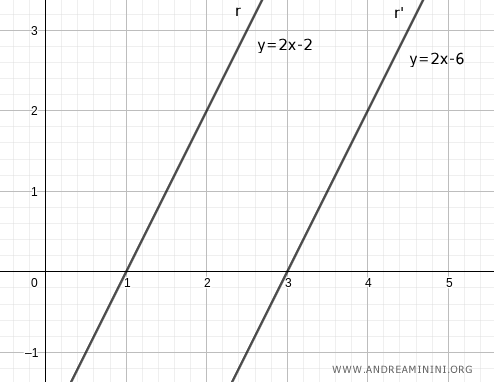
Chiamo i punti di intersezione delle rette sull'asse delle ascisse x1 e x1'.
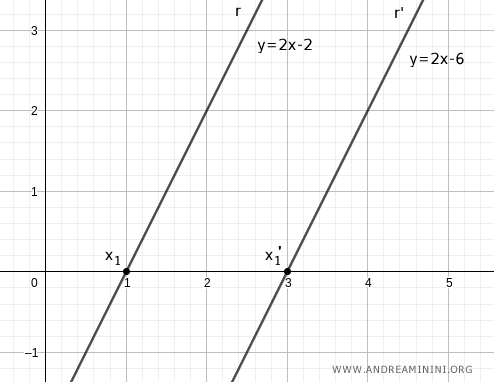
Individuo altri due punti sull'asse delle ascisse sommando a x1 e x1' una costante k. Ad esempio k=1.
$$ x_2=x_1+k $$
$$ x_2'=x_1'+k $$
Pertanto i due segmenti x1x2 e x1'x2' hanno la stessa lunghezza.
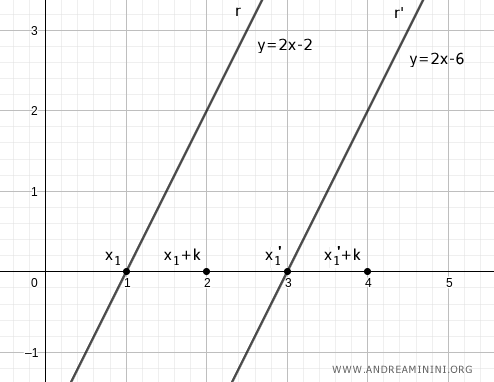
Traccio una retta perpendicolare a partire da x1+k e x1'+k che interseca la rispettiva retta r e r'.
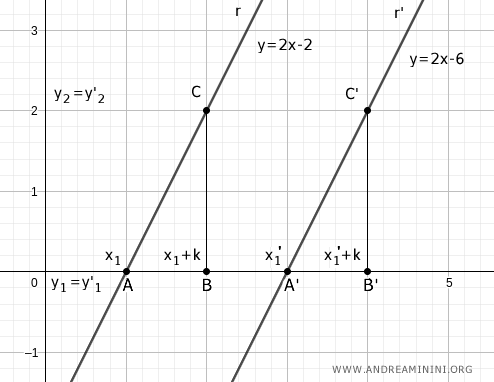
In questo modo si formano due triangoli rettangolo ABC e A'B''C'.
Quindi, hanno l'angolo retto (90°) congruente α=α'.
Per il teorema delle rette parallele sono congruenti anche gli angoli β=β' perché sono angoli corrispondenti, in quanto le rette parallele r e r' sono tagliate dalla stessa trasversale (l'asse x).
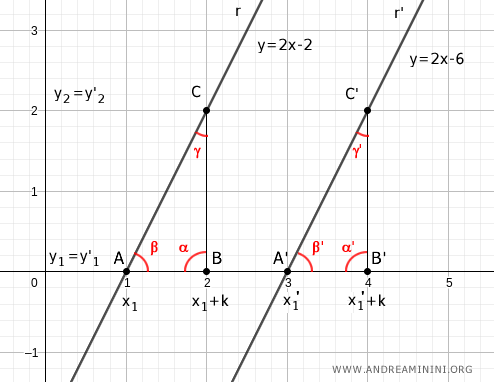
Per il secondo criterio di congruenza i due triangoli sono congruenti ABC≅A'B'C' perché hanno un lato congruente AB≅A'B' per costruzione e gli angoli adiacenti congruenti α≅α' e β≅β'.
Nota. Essendo due triangoli rettangolo, entrambi hanno un angolo è di 90° ( α=α' ). Entrambi hanno un angolo ( β=β' ) determinato dalla stessa trasversale che interseca l'asse delle ascisse. Di conseguenza, anche il terzo angolo deve essere congruente ( γ=γ' ) perché la somma degli angoli in un triangolo rettangolo è pari a 180°.
I due triangoli sono congruenti ABC≅A'B'C', questo significa che hanno tutti i lati della stessa lunghezza.
Quindi i due cateti del triangolo rettangolo sono congruenti.
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
Sapendo che AB=x2-x1 e A'B'=x'2-x'1 (dove x2=x1+k e x'2=x'1+k) e che BC=y2-y1 e A'B'=y'2-y'1
$$ x_2 - x_1 = x'_2-x'_1 $$
$$ y_2 - y_1 = y'_2-y'_1 $$
Il coefficiente angolare è determinato dal rapporto dei due cateti del triangolo rettangolo
$$ m = \frac{y_2-y_1}{x_2-x_1} $$
$$ m' = \frac{y'_2-y'_1}{x'_2-x'_1} $$
Essendo i lati uguali anche il coefficiente angolare è lo stesso.
$$ m = m' $$
Dimostrazione del teorema inverso. Il ragionamento si può fare anche all'inverso. Partendo dall'ipotesi che due rette con lo stesso coefficiente angolare m=m' posso dimostrare che le due rette sono parallele.
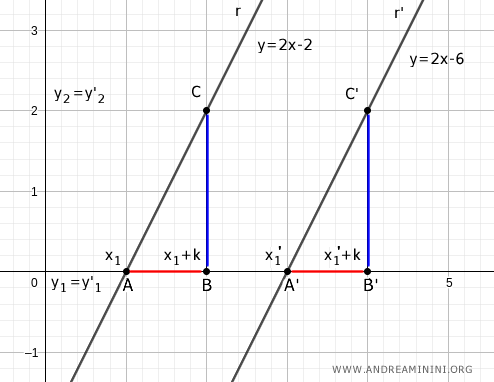
Se due rette hanno lo stesso coefficiente angolare $$ m=m' $$ poiché m=BC/AB e m'=B'C'/A'B', vale la seguente uguaglianza $$ \frac{\overline{BC}}{\overline{AB}} = \frac{\overline{B'C'}}{\overline{A'B'}} $$ Dove AB e A'B' sono segmenti sulle ascisse mentre BC e B'C' sono segmenti sulle ordinate. Se i segmenti sull'ascisse AB≅A'B' sono congruenti, ottengo che anche i segmenti sulle ordinate BC≅B'C' lo sono.

Pertanto i triangoli rettangolo ABC≅A'B'C' sono congruenti per il primo criterio di congruenza dei triangoli, perché hanno due lati congruenti AB≅A'B' e BC≅B'C' e l'angolo tra di essi α≅α' (90°) congruente. Di conseguenza i triangoli ABC≅A'B'C' hanno tutti gli angoli uguali. In particolar modo, mi interessa sapere che sono congruenti gli angoli β≅β' che misurano la pendenza delle rette r e r' rispetto all'asse x, perché questo mi permette di dedurre che le due rette hanno la stessa pendenza rispetto all'asse x ovvero sono rette parallele r // r'.
La condizione di parallelismo delle rette
Due rette $ r $ e $ s $ con le seguenti equazioni in forma implicita $$ r: \ ax+by+c=0 $$ $$ s: \ a'x+b'y+c'=0 $$ sono parallele $ r // s $ se i coefficienti delle equazioni soddisfano la seguente condizione $$ ab' - a'b = 0 $$ che può essere scritta anche in questa forma equivalente $$ \frac{a}{a'} = \frac{b}{b'} $$
Questa condizione è detta condizione di parallelismo delle rette.
Esempio
Prendo come esempio due rette paralle $ r // s $ con le seguenti equazioni in forma implicita.
$$ r: \ 2x+3y+1=0 $$
$$ s: \ 4x+6y-8=0 $$
Verifico se le due rette soddisfano la condizione di parallelismo.
$$ ab' - a'b = 0 $$
In questo caso a=2, b=3, a'=4 e b'=6.
$$ 2 \cdot 6 - 4 \cdot 3 = 0 $$
$$ 12 - 12 = 0 $$
La condizione di parallelismo è soddisfatta, quindi le due rette sono parallele $ r // s $.
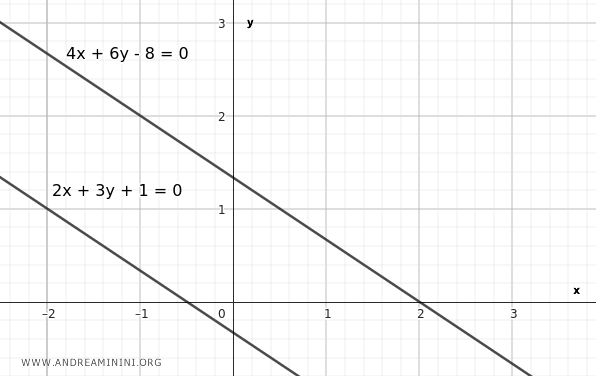
Dimostrazione
Considero due rette paralle $ r // s $ con le seguenti equazioni in forma implicita.
$$ r: \ ax+by+c=0 $$
$$ s: \ a'x+b'y+c'=0 $$
I coefficienti angolari delle due rette sono:
$$ m = - \frac{a}{b} $$
$$ m' = - \frac{a'}{b'} $$
Essendo rette parallele per l'ipotesi iniziale, i due coefficienti angolari sono uguali
$$ m = m' $$
$$ - \frac{a}{b} = - \frac{a'}{b'} $$
Con qualche semplice passaggio algebrico ottengo la condizione di parallelismo tra le rette.
$$ \frac{a}{b} = \frac{a'}{b'} $$
$$ ab' = a'b $$
E questo conclude la dimostrazione.
Come capire se due rette sono parallele distinte o coincidenti
Due rette sono parallele distinte se le equazioni soddisfano la condizione di parallelismo ma non soddisfano la condizione di coincidenza. $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$ Viceversa, se soddisfano entrambe le condizioni sono rette coincidenti. $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$
Sia le rette parallele distinte che quelle coincidenti soddisfano la condizione di parallelismo:
$$ \frac{a}{a'} = \frac{b}{b'} $$
Dove a,a',b,b' sono i coefficienti delle variabili x e y di due rette:
$$ r: ax+by+c=0 $$
$$ r': a'x+b'y+c'=0 $$
In altre parole, le rette coincidenti sono un caso particolare di rette parallele perché hanno la stessa pendenza (coefficiente angolare).
Per capire se due rette parallele sono distinte o coincidenti, devo analizzare anche la condizione di coincidenza tramite il rapporto dei loro termini noti $ \frac{c}{c'} $ .
- Coincidenti
Se il rapporto tra i termini noti è proporzionale a quello dei coefficienti, allora le rette sono coincidenti, ovvero hanno tutti i punti in comune $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$ - Parallele e distinte
Se il rapporto tra i termini noti è diverso da quello dei coefficienti, allora le rette sono parallele distinte, ovvero non hanno nessun punto in comune $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$
Esempio
Considero due rette con le equazioni in forma impropria
$$ r:2x+3y+6=0 $$
$$ r′:4x+6y+12=0 $$
Devo scoprire se sono incidenti, parallele o coincidenti.
Per prima cosa verifico se la condizione di parallelismo è soddisfatta.
$$ \frac{a}{a'} = \frac{b}{b'} $$
In questo caso i coefficienti delle variabili x e y sono a=2, b=3 nella prima equazione e a'=4 e b'=6 nella seconda equazione.
$$ \frac{2}{4} = \frac{3}{6} $$
$$ \frac{1}{2} = \frac{1}{2} $$
La condizione di parallelismo è soddisfatta, ora so per certo che le due rette non sono incidenti.
Devo però capire se sono parallele distinte o coincidenti.
Per farlo analizzo la condizione di coincidenza tramite il rapporto tra i termini noti c=6 e c'=12 delle due equazioni.
$$ \frac{c}{c'} = \frac{6}{12} = \frac{1}{2} $$
Tutti i rapporti sono uguali a 1/2, quindi le due rette sono coincidenti.
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{1}{2} $$
In altre parole, le due rette hanno in comune tutti i punti.
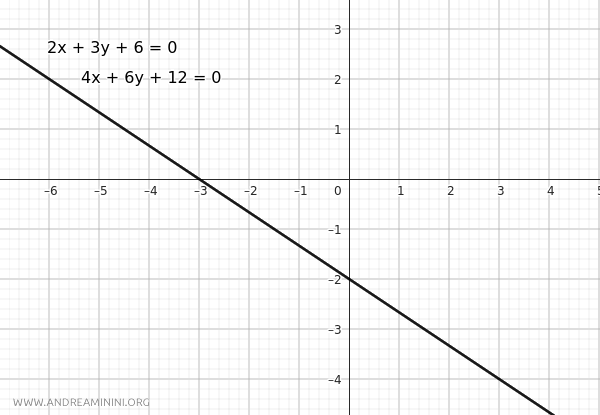
Questi semplici passaggi mi permettono di determinare con precisione la relazione tra due rette in base ai loro coefficienti, senza dover risolvere un sistema di equazioni.
Esempio di rette parallele e distinte. Per completezza faccio anche un altro esempio in cui due rette sono parallele distinte. Prendo il caso di queste due rette. $$ r:2x+3y+6=0 $$ $$ r′:4x+6y+3=0 $$ Le equazioni sono simili al precedente esempio. La condizione di parallelismo è soddisfatta: $$ \frac{a}{a'} = \frac{b}{b'} $$ $$ \frac{2}{4} = \frac{3}{6} $$ $$ \frac{1}{2} = \frac{1}{2} $$ Tuttavia, in questo caso la condizione di coincidenza non è soddisfatta perché il rapporto tra i termini noti è uguale a 2. $$ \frac{c}{c'} = \frac{6}{3} = 2 $$ Quindi il rapporto c/c' noti non è proporzionale al rapporto tra i coefficienti delle variabili. $$ \frac{a}{a'} = \frac{b}{b'} = \frac{1}{2} \ne 2 = \frac{c}{c'} $$ Pertanto le due rette sono parallele e distinte.
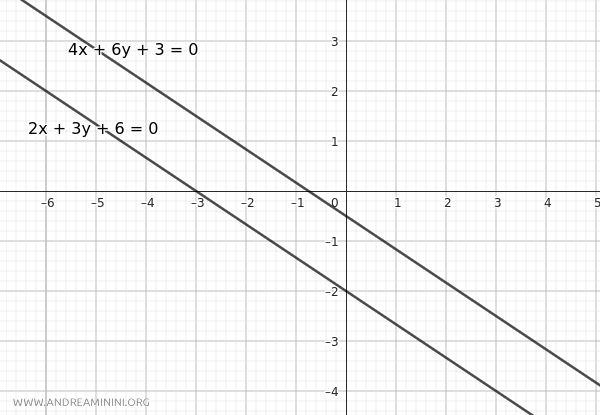
Osservazioni
Alcune osservazioni sulle rette parallele
- La distanza tra due rette parallele è costante in ogni punto di ciascuna retta
I segmenti perpendicolari condotti da due punti di una retta $ r $ a una retta $ s $ parallela a $ r $, sono segmenti congruenti.
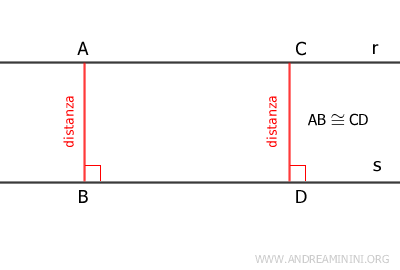
In altre parole, date due rette parallele, la distanza tra le due rette è la stessa in ogni punto.
Dimostrazione. Se considero due rette parallele r // s, essendo le rette perpendicolari a una retta sono perpendicolari anche all'altra retta. Quindi, se prendo due segmenti AB e CD perpendicolari alle rette r e s, questi formano un rettangolo ABCD. In un rettangolo i lati opposti sono congruenti, quindi i segmenti AB≅CD sono congruenti. Questo dimostra che la distanza (altezza) tra due rette parallele è costante in qualsiasi punto.
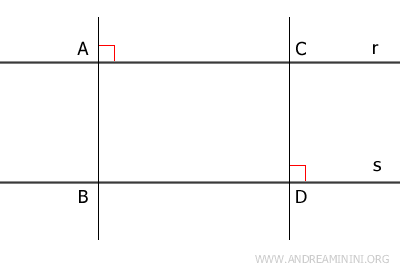
Dimostrazione alternativa. Considero due rette parallele $ r $ e $ s $, due punti distinti qualsiasi $ A $ e $ C $ della retta $ r $ e le proiezioni dei punti $ B $ e $ D $ sulla retta $ s $. Poi traccio il segmento $ AD $.
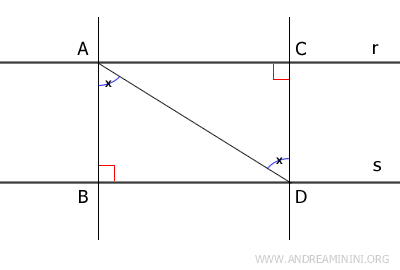
I due triangoli sono congruenti $ \triangle ABD \cong \triangle ACD $ per il secondo criterio generalizzato di congruenza (ALA) perché hanno un lato coincidente $ AD $, un angolo di 90° e due angoli congruenti, in quanto alterni interni di una trasversale tra due rette parallele, nello stesso ordine. Quindi, hanno tutti i lati congruenti tra cui $ AB \cong CD $. Questo dimostra che la distanza tra le rette parallele è la stessa in ogni punto delle rette. - Due rette r e s perpendicolari a una terza retta t sono rette parallele
Le rette r e s formano coppie di angoli corrispondenti congruenti. Pertanto, per il teorema delle rette parallele sono rette parallele.
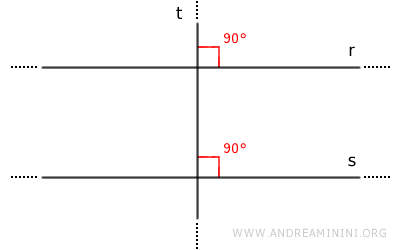
In alternativa, posso dire che le rette r e s formano coppie di angoli alterni interni (o esterni) congruenti oppure coppie di angoli coniugati supplementari. In tutti i casi la conclusione è il parallelismo tra le due rette.
Dimostrazione. Considero due rette $r$ e $s$ perpendicolari a una stessa retta $t$. Procedo per assurdo: suppongo che $r$ e $s$ siano incidenti, cioè non parallele. In tal caso, le due rette si intersecherebbero in un punto $P$ comune. Ma ciò implicherebbe l’esistenza di due rette distinte, entrambe perpendicolari alla stessa retta $t$ e passanti per lo stesso punto $P$, in contraddizione con il teorema dell’unicità della perpendicolare. Quindi l’ipotesi è falsa e posso concludere che le rette $r$ e $s$ sono parallele.
- Il postulato delle rette parallele (quinto postulato di Euclide)
Per un punto P esterno a una retta r passa una e una sola retta parallela a r.
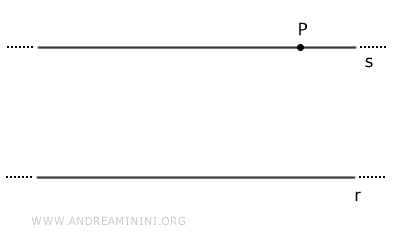
- Una retta t perpendicolare alla retta r è anche perpendicolare a tutte le parallele della retta r
Date due rette parallele r e s, se la retta t è perpendicolare a una retta, allora è perpendicolare anche all'altra retta.
Dimostrazione. Considero due rette parallele r//s e una terza retta t perpendicolare alla retta s. Quindi, per l'ipotesi iniziale le rette t e s formano un angolo α=90°.
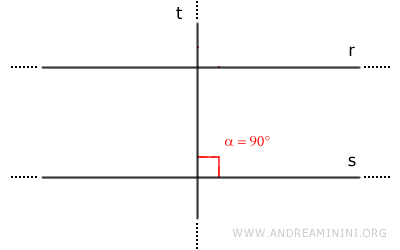
Le due rette r e s sono rette parallele r//s. Quindi, per il teorema delle rette parallele le rette r e s formano due coppie di angoli corrispondenti congruenti rispetto alla stessa retta trasversale (α≅β). Pertanto, anche l'angolo β è un angolo retto (β=90°).
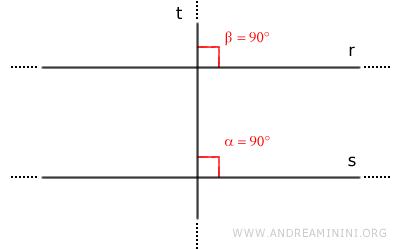
Di conseguenza, la retta t è perpendicolare anche alla retta r. - Le rette parallele di due rette incidenti a e b sono anch'esse incidenti
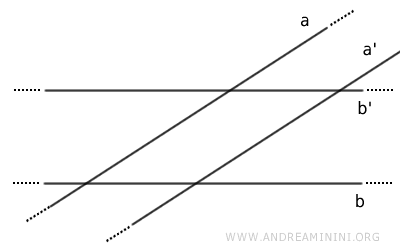
Dimostrazione. Per assurdo, date due rette a e b incidenti, le loro rispettive rette parallele a' e b' sono parallele tra loro a' // b' $$ a \parallel a' $$ $$ b \parallel b' $$ $$ a' \parallel b' $$ Se le rette a' e b' sono parallele tra loro (a' // b') per la proprietà transitiva dovrebbero essere parallele anche le rette a // b $$ a' \parallel b' \ , \ b' \parallel b \Rightarrow a \parallel b $$ Questo però contraddice l'ipotesi iniziale, in base alla quale le rette a e b sono incidenti. Quindi l'affermazione è falsa. E' vero il suo contrario, ossia date due rette a e b incidenti, sono incidenti anche le loro rispettive parallele a' e b'.
- Teorema dei piani paralleli intersecati da un terzo piano
Se un piano \( \pi \) interseca due piani paralleli \( \pi_1 \) e \( \pi_2 \), le intersezioni sono due rette parallele.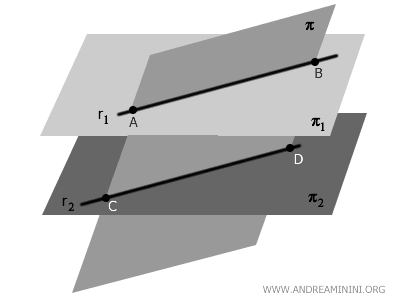
Questo accade perché se un piano \( \pi \) interseca due piani paralleli \( \pi_1 \) e \( \pi_2 \), le intersezioni sono due rette \( r_1 \) e \( r_2 \). Poiché \( \pi_1 \) e \( \pi_2 \) sono equidistanti e \( \pi \) li taglia con lo stesso angolo, le rette \( r_1 \) e \( r_2 \) risultano parallele.
E così via.
