Teorema del sottospazio del prodotto
Se prendo due sottoinsiemi \(A\) e \(B\) di spazi topologici rispettivamente \( X\) e \( Y\) $$ A \subset X $$ $$ B \subset Y $$ la topologia sul prodotto \(A \times B\) come sottospazio di \(X \times Y\) è la stessa della topologia prodotto su \(A \times B\) costruita usando le topologie di \(A\) e \(B\) ereditate da \(X\) e \(Y\). $$ \quad \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$
Dove \(\tau_{A \times B}^{\text{sub}}\) è la topologia di sottospazio su \(A \times B\) derivata da \(X \times Y\),
Mentre \(\tau_A^{\text{sub}}\) e \(\tau_B^{\text{sub}}\) sono le topologie di sottospazio su \(A\) e \(B\) derivate rispettivamente da \(X\) e \(Y\).
In sostanza, questo teorema afferma che i due modi di definire la topologia su \(A \times B\) portano allo stesso risultato.
La topologia su \(A \times B\) derivata come sottospazio di \(X \times Y\) è identica alla topologia che otterrei costruendo direttamente la topologia prodotto su \(A \times B\) a partire dalle topologie di \(A\) e \(B\).
Quindi non importa quale metodo uso, otterrò comunque la stessa struttura topologica su \(A \times B\).
Un esempio pratico
Provo a spiegare meglio il teorema con un esempio.
Considero due spazi topologici \(X\) e \(Y\). Un esempio potrebbe essere il piano cartesiano, dove \(X\) è l'asse \(x\) e \(Y\) è l'asse \(y\).
Ora considero due sottoinsiemi di questi spazi: \(A\) è un sottoinsieme di \(X\) e \(B\) è un sottoinsieme di \(Y\).
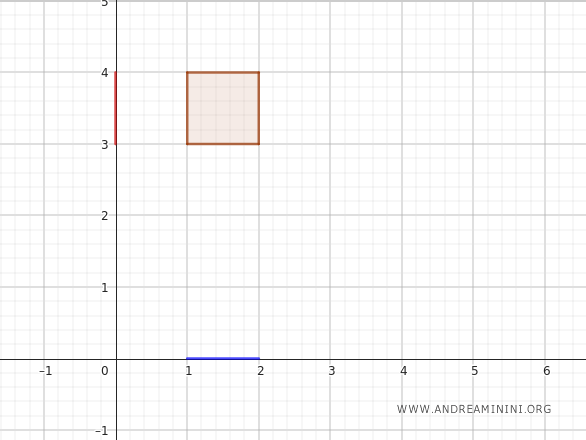
Ad esempio, \(A\) potrebbe essere un intervallo sull'asse \(x\), diciamo \([1, 2]\), e \(B\) potrebbe essere un intervallo sull'asse \(y\), diciamo \([3, 4]\).
Il prodotto cartesiano di questi due sottoinsiemi \(A \times B\) consiste in tutte le coppie \((x, y)\) dove \(x\) è preso da \(A\) e \(y\) è preso da \(B\).
In questo esempio, il prodotto cartesiano è un rettangolo nel piano, con \(x\) che va da 1 a 2 e \(y\) che va da 3 a 4.
Ora, possmo considerare due diverse topologie su \(A \times B\):
- Topologia come sottospazio
Considero \(A \times B\) come un sottospazio del prodotto \(X \times Y\), dove \(X \times Y\) è l'intero piano. Questo significa che eredito la topologia di \(X \times Y\) e poi la restringo al sottoinsieme \(A \times B\). - Topologia prodotto
Posso anche costruire direttamente una topologia su \(A \times B\) usando le topologie di \(A\) e \(B\). In questo caso, considero \(A\) come uno spazio topologico con la topologia ereditata da \(X\) e \(B\) come uno spazio topologico con la topologia ereditata da \(Y\), e poi creo la topologia prodotto su \(A \times B\).
Queste due topologie, quella del sottospazio e quella prodotto, sono in realtà la stessa cosa.
Quindi non importa quale metodo si usa, otterrò la stessa struttura topologica su \(A \times B\).
E così via
