Teorema dell'interno del prodotto cartesiano
Due insiemi \(A\) e \(B\) appartenenti a due spazi topologici \(X\) e \(Y\) rispettivamente, l'interno del prodotto cartesiano \(A \times B\) è uguale al prodotto degli interni di \(A\) e \(B\). In altre parole: $$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$
E' una proprietà specifica degli insiemi aperti nel contesto del prodotto di due spazi topologici.
Questo teorema dice che per insiemi \(A\) e \(B\) in spazi topologici \(X\) e \(Y\), l'interno del loro prodotto cartesiano può essere trovato semplicemente prendendo il prodotto degli interni di \(A\) e \(B\).
Un esempio pratico
Considero due spazi topologici \(X = \mathbb{R}\) e \(Y = \mathbb{R}\) e due sottoinsiemi \(A = (0, 2)\) e \(B = (1, 3)\).
Dove \(A\) e \(B\) sono intervalli aperti nella retta reale \(\mathbb{R}\).
Calcolo l'interno dei due insiemi
L'interno di \( A \) è (0,2) siccome \(A\) è già un intervallo aperto, quindi il suo interno è semplicemente \(A\) stesso.
$$ \text{Int}(A) = (0, 2) $$
Allo stesso modo l'interno di \( B \) è (1,3)
$$ \text{Int}(B) = (1, 3) $$
Ora calcolo il prodotto cartesiano degli interni \(\text{Int}(A) \times \text{Int}(B)\):
$$ \text{Int}(A) \times \text{Int}(B) = (0, 2) \times (1, 3) $$
Questo prodotto cartesiano è l'insieme di tutte le coppie \((x, y)\) dove \(x \in (0, 2)\) e \(y \in (1, 3)\).
$$ \text{Int}(A) \times \text{Int}(B) = \{(x, y) \mid x \in (0, 2) \text{ e } y \in (1, 3) $$
Questo insieme può essere anche visto come un rettangolo aperto nel piano \(\mathbb{R}^2\), definito dagli estremi \((0, 1)\), \((0, 3)\), \((2, 1)\), e \((2, 3)\).
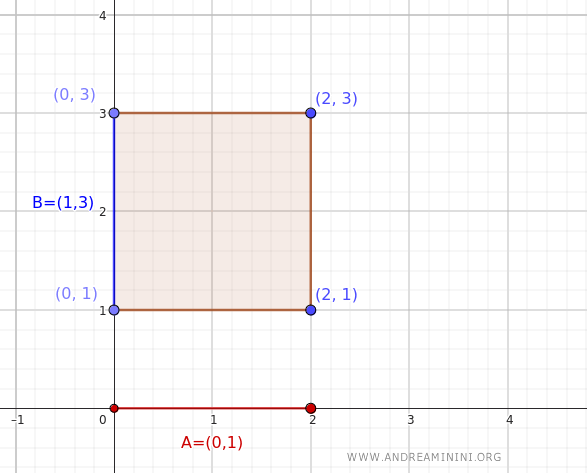
A questo punto calcolo l'interno del prodotto cartesiano \(A \times B = (0, 2) \times (1, 3) \):
Questo è lo stesso insieme di prima, il rettangolo aperto nel piano \(\mathbb{R}^2\).
L'interno del prodotto cartesiano \(\text{Int}(A \times B)\) è esattamente uguale al prodotto degli interni \(\text{Int}(A) \times \text{Int}(B)\).
$$ \text{Int}(A \times B) = (0, 2) \times (1, 3) = \text{Int}(A) \times \text{Int}(B) $$
Questo esempio conferma il teorema.
Dimostrazione
La dimostrazione è divisa in due parti. Prima bisogna dimostrare che l'interno del prodotto cartesiano contiene il prodotto degli interni e poi che è contenuto nel prodotto degli interni, dimostrando così che sono uguali.
1] L'interno del prodotto cartesiano contiene il prodotto degli interni
In questa prima parte devo dimostrare che
$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$
In altre parole, devo dimostrare che ogni coppia \((x, y)\) dove \(x \in \text{Int}(A)\) e \(y \in \text{Int}(B)\) appartiene all'interno di \(A \times B\).
Siccome \(x \in \text{Int}(A)\) è un elemento dell'interno di $ A $, so che esiste un insieme aperto \(U\) contenuto in \(X\) tale che \(x \in U \subseteq A\).
Allo stesso modo, poiché \(y \in \text{Int}(B)\) è un elemento dell'interno di $ B $, esiste un insieme aperto \(V\) contenuto in \(Y\) tale che \(y \in V \subseteq B\).
Il prodotto \(U \times V\) è un insieme aperto nel prodotto topologico \(X \times Y\) e contiene la coppia \((x, y)\).
Dato che \(U \times V\) è contenuto in \(A \times B\), questo dimostra che \((x, y)\) appartiene a \(\text{Int}(A \times B)\).
Quindi ho dimostrato che \(\text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B)\).
2] Il prodotto degli interni contiene l'interno del prodotto cartesiano
Ora devo dimostrare che
$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$
In altre parole, devo dimostrare che se \((x, y) \in \text{Int}(A \times B)\), allora \(x \in \text{Int}(A)\) e \(y \in \text{Int}(B)\).
Prendo una coppia di punti \((x, y)\) appartenente a \(\text{Int}(A \times B)\).
Questo significa che esiste un insieme aperto \(W\) contenuto in \(X \times Y\) tale che \((x, y) \in W \subseteq A \times B\).
Nel prodotto topologico, posso trovare insiemi aperti \(U\) e \(V\) in \(X\) e \(Y\) rispettivamente, tali che \(W\) contiene un prodotto cartesiano \(U \times V\) con \((x, y) \in U \times V \subseteq W\).
Poiché \(U \times V \subseteq A \times B\), deduco che \(U\) è contenuto in \(A\) e \(V\) è contenuto in \(B\).
Ciò significa che \(x \in U \subseteq A\) e \(y \in V \subseteq B\), quindi \(x\) appartiene all'interno di \(A\) e \(y\) appartiene all'interno di \(B\).
Pertanto, \((x, y) \in \text{Int}(A) \times \text{Int}(B)\), il che dimostra che \(\text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B)\).
3] Conclusione
Ho dimostrato entrambe le inclusioni:
$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$
$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$
Quindi posso concludere che l'interno del prodotto $ A \times B $ è uguale al prodotto degli interni di $ A $ e $ B $
$$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$
E così via.
