Le reti di Petri

Le reti di Petri sono un modello di sistemi a eventi discreti. Sono usate per rappresentare gli eventi di un sistema secondo l'ordine in cui si presentano. Per questa ragione sono anche dette reti posto/transizione o P/T.

Perché si chiamano reti di Petri?

Prendono il nome del loro autore. Sono state ideate dal ricercatore tedesco Karl Adam Petri negli anni '60.

Ecco un esempio pratico di rete di Petri.

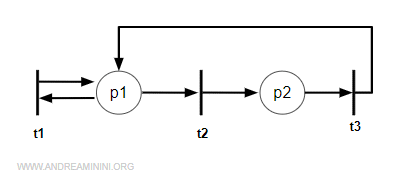
Nota. In genere una rete di Petri è un modello logico di sistema a eventi discreti (SED) che non prende in considerazione il tempo. Tuttavia, esistono anche tipologie di reti di Petri temporizzate. Inoltre, la rete posto/transizione è soltanto una tipologia di rete di Petri, la più semplice.

Come funziona la rete di Petri

Una rete di Petri del tipo posto/transizione (o rete P/T) è una struttura composta da due insiemi e due matrici. $$ N = \{ P,T,Pre, Post \} $$

La rappresentazione grafica è un grafo orientato (digrafo) con archi pesati formato da posti e transizioni.

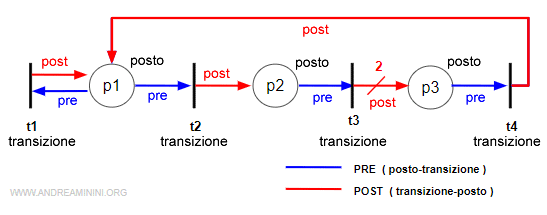
I posti (p) sono sono rappresentati da cerchi. Formalmente l'insieme dei posti è indicato con la lettera P. $$ P = \{ p_1, p_2, p_3, ... \} $$

Le transizioni (t) sono rappresentate da barre o da rettangoli. Formalmente, l'insieme delle transizioni è indicato con la lettera T. $$ T = \{ t_1, t_2, t_3, ... \} $$

Nota. Sia i posti che le transizioni sono nodi del digrafo. Sono indicati con un simbolo diverso per distinguerli tra loro. Si presume che P e T siano insiemi disgiunti ossia P⋂T=ø

Gli archi dai posti alle transizioni sono detti archi pre-incidenza e sono rappresentati da una matrice Pre (p,t).

Si chiama "Pre" perché conta gli archi in entrata (input) delle transizioni.

Gli archi dalle transizioni ai posti sono detti archi post-incidenza e sono rappresentati da una matrice Post(p,t).

Si chiama "Post" perché conta gli archi in uscita (output) delle transizioni.

Nota. In entrambi i casi i posti sono disposti in riga mentre le transizioni sono disposte in colonna. Gli elementi della matrice sono interi non negativi che indicano la presenza dell'arco (1) o l'assenza (0). Se l'intero è un numero maggiore di 1, il numero indica la quantità di archi.

Spesso le due matrici Pre e Post sono unite in un'unica matrice in forma compatta, detta matrice di incidenza.

$$ C=Post-Pre = \begin{pmatrix} 1-1 & 0-1 & 0 & 1 \\ 0 & 1 & 0-1 & 0-1 \\ 0 & 0 & 2 & 0-1 \end{pmatrix} = \begin{pmatrix} 0 & -1 & 0 & 1 \\ 0 & 1 & -1 & -1 \\ 0 & 0 & 2 & -1 \end{pmatrix} $$

Ogni elemento della matrice di incidenza è la somma algebrica dei rispettivi elementi nelle matrici Post e Pre.

$$ C(p,t)=Post(p,t)-Pre(p,t) $$

Nota. La forma comporta una perdita di informazioni. Ad esempio, se un posto e una transizione hanno un eguale numero di archi reciproci tra loro (cappio) nella matrice di incidenza la differenza è comunque pari a zero, come se non ci fosse nulla. In pratica, la rete appare sempre senza cappi (rete pura) anche se ci sono.

A ogni elemento è associato un insieme con gli elementi associati in entrata e in uscita.

Generalmente si mette il simbolo star prima dell'elemento (*n) per indicare i collegamenti in entrata, dopo il nome (n*) per quelli in uscita.

Esempio. Il posto p₁ ha i seguenti collegamenti in entrata *p₁={t₁,t₄} e in uscita p₁*={t₁,t₂}. Lo stesso si può fare per le transizioni. La transizione t1 ha i seguenti collegamenti in entrata *t₁={p₁} e in uscita t₁*={p₁}.

Un esempio pratico

Ho una rete composta da tre posti

$$ P = \{ p_1, p_2, p_3 \} $$

e da quattro transizioni

$$ T = \{ t_1, t_2, t_3, t_4 \} $$

La matrice pre-incidenza (posti-transizioni) conta gli archi in entrata nelle transizioni ed è la seguente

$$ Pre = \begin{pmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} $$

La matrice post-incidenza (transizioni-posti) conta gli archi in uscita dalla transizioni ed è la seguente

$$ Post = \begin{pmatrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \end{pmatrix} $$

Per rappresentare il digrafo disegno un cerchio per ogni posto P e una barra (o rettangolo) per ogni transizione T.

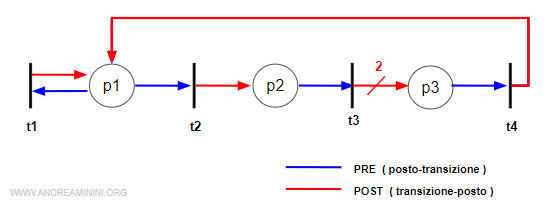
Poi li collego tra loro con degli archi orientati secondo le indicazioni delle matrici pre e post incidenza.

• Per ogni intero positivo della matrice di pre-incidenza aggiungo nel digrafo un arco di colore rosso dal posto alla transizione.
• Per ogni intero positivo della matrice di post-incidenza aggiungo nel digrafo un arco di colore blu dalla transizione al posto.

Nota. Gli elementi uguali a zero nella matrice indicano l'assenza dell'arco. Quindi, li ignoro. Viceversa la presenza di un intero positivo indica la presenza dell'arco. Se l'intero n è maggiore di 1, vuol dire che ci sono n archi da disegnare. In questo caso è preferibile scrivere un solo arco barrato e aggiungere il numero degli archi sopra ( ad esempio l'arco che congiunge la transizione t3 con il posto p3 è composto da 2 archi ). In questo modo il digrafo è più sintetico e compatto.

La rete marcata

Alla reti di Petri può essere aggiunta una marcatura.

La marcatura indica lo stato corrente della rete posto-transizione (P/T). E' una funzione che associa a ogni posto un numero intero non negativo.

Le marche sono indicate in un vettore M con tanti elementi quanti sono i posti della rete.

$$ M = \{ m_1, m_2, m_3, ... \} $$

Dal punto di vista grafico si indica con un pallino (o gettone) nel posto.

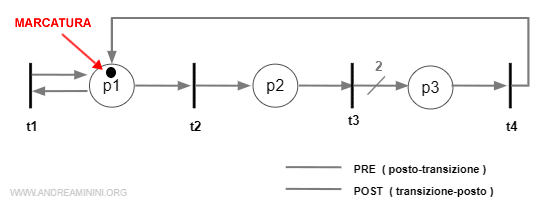
Un esempio pratico

Questo vettore associa una marca al posto p₂, due marche al posto p₄ e zero agli altri posti della rete.

$$ M = \{ 0, 1, 0, 2 \} $$

La rete marcata

Una rete P/T posto-transizione è detta rete marcata (o sistema di rete) se ai posti è associata una marcatura iniziale M₀ che ne definisce lo stato. $$ <N, M_0> $$

La rete marcata ha uno stato predefinito anche nel momento iniziale che influisce sulla sua evoluzione dinamica.

Quali sono i vantaggi delle rete di Petri

Le reti di Petri hanno i seguenti vantaggi

• La rappresentazione grafica delle reti di Petri è molto compatta (sintetica) e mi consente di comprendere più facilmente l'evoluzione e il funzionamento di un sistema.

  Esempio. Una rete di Petri non rappresenta tutti gli stati del sistema ma soltanto le regole di evoluzione del sistema. Questa proprietà è molto utile perché mi permette di rappresentare anche sistemi discreti con infiniti stati. Il che è un bel vantaggio rispetto agli automi.

• Le reti di Petri sono anche un modello matematico e mi permettono di analizzare la rete tramite gli strumenti dell'algebra lineare. Non sono soltanto una rappresentazione grafica del sistema.
• La rappresentazione di una rete di Petri è modulare. Ogni parte del sistema posso considerarla come sottosistema indipendente ( modulo ) e analizzarlo in modo indipendente dagli altri.
• Le reti di Petri mi permettono anche di analizzare più facilmente le attività che si svolgono contemporaneamente e i sistemi caratterizzati dalla parallelizzazione delle attività.

E così via.