La sequenza di transizioni abilitate nella rete di petri
In una rete di Petri una sequenza di transizioni abilitate $$ s=t_1,t_2, ..., t_n $$ indica una possibile dinamica del sistema a partire da una marcatura iniziale M.
E' anche detta sequenza di scatto.
Un esempio pratico
In questa rete marcata <N,M> ci sono due transizioni abilitate t2 e t3
La marcatura iniziale è M = [1 0 0]
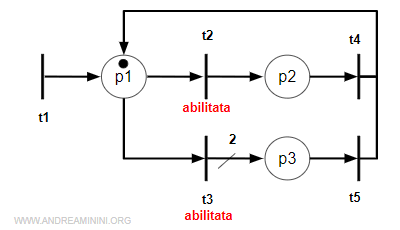
La rete può scattare verso t2 o verso t3
Ad esempio, il primo scatto è verso la transizione t2
$$ M[t_2>M^{(1)} $$
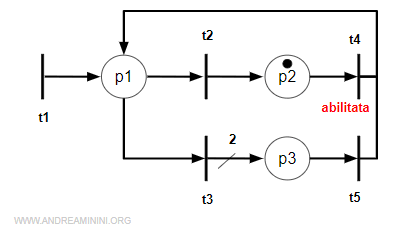
Ora l'unica transizione abilitata è la t4 e la marcatura è.
$$ M^{(1)} = [ 0 1 0 ] $$
Il secondo scatto è verso la transizione t4 e il sistema torna nuovamente al posto p1.
$$ M^{(1)}[t_4>M^{(2)} $$

La marcatura corrente è
$$ M^{(2)} = [ 1 0 0 ] $$
Ora scatta la transizione t3
$$ M^{(2)}[t_3>M^{(3)} $$
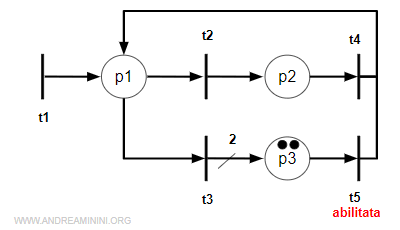
La marcatura corrente è
$$ M^{(3)} = [ 0 0 2 ] $$
Poi la transizione t5
$$ M^{(3)}[t_5>M^{(4)} $$
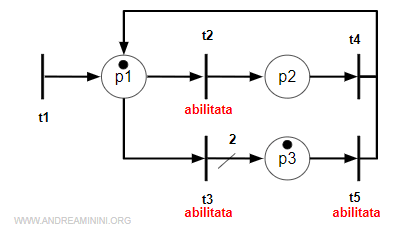
La marcatura finale è
$$ M^{(4)} = [ 1 0 1 ] $$
Il sistema ha compiuto una sequenza σ di transizioni abilitate
$$ σ = t_2 , t_4 , t_3 , t_5 $$
Nota. Per indicare che la sequenza σ è stata abilitata dalla marcatura M posso scrivere $$ M[σ> $$ Posso eventualmente anche indicare la marcatura finale $$ M[σ>M^{(4)} $$
Alla sequenza corrisponde una traiettoria
$$ M[t_2>M^{(1)}[t_4>M^{(2)}[t_3>M^{(3)}[t_5>M^{(4)} $$
Nota. La sequenza può anche essere più lunga e contenere una stessa transizione ripetuta più volte al suo interno. In questo esempio ho limitato la sequenza ha quattro scatti per semplicità.
Ovviamente è soltanto una sequenza abilitata tra le tante dinamiche ed evoluzioni possibili a partire da una marcatura iniziale M0.
Ad esempio, altre sequenze possibili dell'esempio precedente sono
$$ σ' = t_2 , t_4 , t_2 , t_4 \\ σ" = t_3 , t_5 , t_2 , t_4 \\ \vdots $$
L'insieme di tutte le sequenze abilitate dalla marcatura iniziale è detta comportamento (o linguaggio) della rete marcata.
$$ L(N,M_0) $$
La sequenza vuota
Una sequenza vuota ε di transizioni abilitate indica che non ci sono stati scatti.
Pertanto, dopo una sequenza vuota la marcatura della rete di petri resta immutata.
$$ M[ε>M $$
Per definizione la sequenza vuota è abilitata da ogni marcatura.
E così via.
