Vettore P invariante di supporto minimo

Un vettore P-invariante x è di supporto minimo se non esiste un altro P invariante x' tale che $$ || x' || ⊂ ||x|| $$

Un esempio pratico

Ho una rete marcata con tre posti e due transizioni.

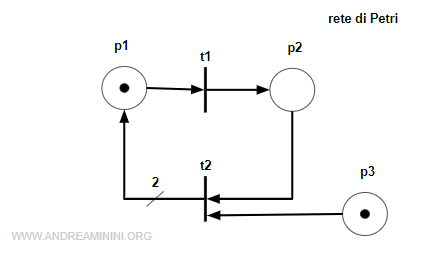
La matrice di incidenza C della rete è uguale alla differenza tra la matrice Post e Pre transizioni.

$$ C =\begin{pmatrix} 0 & 2 \\ 1 & 0 \\ 0 & 0 \end{pmatrix} - \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 0 & 1 \end{pmatrix} $$

$$ C =\begin{pmatrix} -1 & 2 \\ 1 & -1 \\ 0 & -1 \end{pmatrix} $$

In questa matrice esistono diversi vettori P-invarianti tali che

$$ x^T \cdot C = 0 $$

Ad esempio, il vettore x=[1,1,1] è P-Invariante perché moltiplicato per la matrice di incidenza restituisce un vettore nullo come prodotto.

$$ x^T \cdot C = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}^T \cdot \begin{pmatrix} -1 & 2 \\ 1 & -1 \\ 0 & -1 \end{pmatrix} = [1 \: 1 \: 1] \cdot \begin{pmatrix} -1 & 2 \\ 1 & -1 \\ 0 & -1 \end{pmatrix} = [0 \: 0] $$

Il supporto del vettore x è

$$ ||x|| = \{ p_1 \: p_2 \: p_3 \} $$

Cos'è il supporto? Il supporto è un insieme contenente i posti in cui gli elementi del vettore hanno valori non nulli. In questo caso il vettore è x=[1,1,1] quindi tutti i posti sono attivi ||x|| = {p1,p2,p3}

Analizzo l'insieme delle parti del supporto ||x|| per vedere se qualche sottoinsieme non nullo di ||x|| corrisponde a un vettore P-invariante

$$ \{ p_1 \: p_2 \} = [1,1,0]^T \cdot C = [0,1] $$

$$ \{ p_1 \: p_3 \} = [1,0,1]^T \cdot C = [-1,1] $$

$$ \{ p_2 \: p_3 \} = [0,1,1]^T \cdot C = [1,-2] $$

$$ \{ p_1 \} = [1,0,0]^T \cdot C = [-1,2] $$

$$ \{ p_2 \} = [0,1,0]^T \cdot C = [1,-1] $$

$$ \{ p_3 \} = [0,0,1]^T \cdot C = [0,-1] $$

Nessun vettore corrispondente ai sottoinsiemi di ||x|| è P-invariante.

Pertanto, il vettore x=[1,1,1] è un vettore P-invariante di supporto minimo.

E così via.