Analisi della raggiungibilità tramite P-invarianti
L'analisi dei vettori P-invariabili mi consente di approssimare la raggiungibilità di una rete marcata <N,M0>.
Come funziona
Dopo aver calcolato i vettori P-invarianti minimali li dispongo in colonna nella matrice M
$$ M = [ x_1, x_2, ... , x_n ] $$
Poi costruisco l'insieme X invariante della rete, composto da tutti i vettori che soddisfano l'uguaglianza
$$ X^T \cdot M = X^T \cdot M_0 $$
Dove M è una marcatura ottenuta dalla combinazione degli m posti della rete.
L'insieme X-invariante contiene al suo interno anche l'insieme potenzialmente raggiungibile della rete.
$$ R(N,M_0) ⊆ PR(N,M_0) ⊆ I_X(N,M_0) $$
Un esempio pratico
Ho una rete con tre posti e tre transizioni.
La marcatura iniziale è M0=[0 1 1 ].
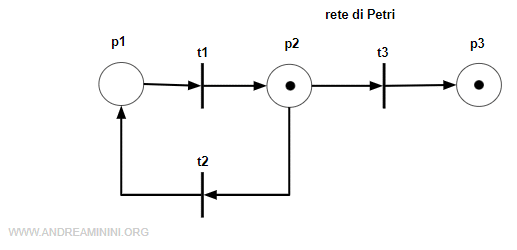
Costruisco la matrice di incidenza della rete per differenza tra la matrice Post e Pre transizione.
$$ C = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} - \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{pmatrix} $$
$$ C = \begin{pmatrix} -1 & 1 & 0 \\ 1 & -1 & -1 \\ 0 & 0 & 1 \end{pmatrix} $$
Questa rete ha un vettore P-invariabile minimale x = [1 1 1]
$$ x^T \cdot C = 0 $$
$$ [ 1 \: 1 \: 1] \cdot \begin{pmatrix} -1 & 1 & 0 \\ 1 & -1 & -1 \\ 0 & 0 & 1 \end{pmatrix} = [ 0 \: 0 \: 0 ] $$
Quindi la matrice X è composta da una colonna
$$ X = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} $$
Ora calcolo l'insieme X-invariante
$$ X^T \cdot M = X^T \cdot M_0 $$
$$ [1 \: 1 \: 1 ] \cdot M = [1 \: 1 \: 1] \cdot M_0 $$
La marcatura iniziale è M0=[0 1 1 ].
$$ [1 \: 1 \: 1 ] \cdot M = [1 \: 1 \: 1] \cdot \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $$
La generica marcatura M è composta da un vettore con tre elementi M(p1), M(p2), M(p3)
$$ [1 \: 1 \: 1 ] \cdot \begin{pmatrix} M(p_1) \\ M(p_2) \\ M(p_3) \end{pmatrix} = [1 \: 1 \: 1] \cdot \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $$
Svolgo le moltiplicazioni riga per colonna
$$ M(p_1) + M(p_2) + M(p_3) = 2 $$
Nota. Le variabili delle marche nei posti della rete M(p1), M(p2), M(p3) sono non negative. Un posto può avere zero, una o più marche. Pertanto, le variabili possono assumere valori positivi o nulli ma non negativi.
Pertanto l'insieme X invariante è composto dai vettori
$$ X = \{ [1 \: 1 \: 0] \:,\: [1 \: 0 \: 1] \:,\: [0 \: 1 \: 1] \:,\: [2 \: 0 \: 0] \:,\: [0 \: 2 \: 0] \:,\: [0 \: 0 \: 2] \: \} $$
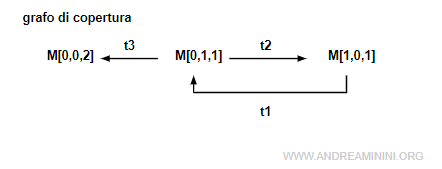
Tra questi ci sono anche le marcature raggiungibili della rete ossia [0 1 1], [1,0,1] e [0 0 2].
Queste sono ben evidenti osservando il grafo di copertura della rete.
Dimostrazione
Se una marcatura è potenzialmente raggiungibile esiste un vettore y tale che
$$ M = M_0 + C \cdot y $$
Pertanto, sostituendo M alla condizione dell'insieme X-invariante
$$ X^T \cdot M = X^T \cdot M_0 $$
$$ X^T \cdot (M_0 + C \cdot y) = X^T \cdot M_0 $$
$$ X^T \cdot M_0 + X^T \cdot C \cdot y = X^T \cdot M_0 $$
Poiché la matrice X-invariante contiene esclusivamente vettori P-invarianti, il prodotto è XCy=0.
Pertanto la marcatura M è inclusa nell'insieme Ix.
E così via.
