Il vettore caratteristico delle reti di Petri
Il vettore caratteristico di una rete di Petri N indica quante volte si verificano le transizioni in una particolare sequenza σ.
E' anche detto vettore di scatto associato.
Un esempio pratico
Una rete N è composta da n=5 transizioni
$$ T= \{ t_1 , t_2, ... , t_5 \} $$
Ecco la rappresentazione grafica
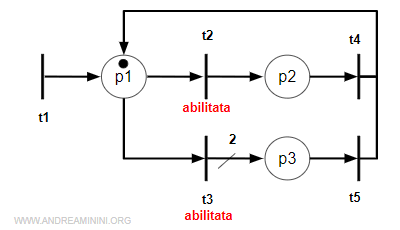
Prendo una sequenza di transizioni σ tra le tante possibili
$$ σ=t_1 t_2 t_4 t_2 $$
Nella sequenza la transizione t2 si ripete due volte mentre t1 e t4 una volta sola. Le transizioni t3 e t5 invece non scattano mai.
Il vettore caratteristico di σ è
$$ σ= [ 1,2,0,1,0 ] $$
Ogni posizione indica una transizione per numero.
Nota. La prima posizione è la transizione t1, la seconda posizione è la transizione t2, la terza t3, la quarta t4, la quinta t5. $$ σ= [ t_1,t_2,t_3,t_4,t_t ] = [ 1,2,0,1,0 ] $$
E così via.
