Le transizioni abilitate nella rete di Petri

In una rete di Petri una transizione (t) è detta transizione abilitata se ogni posto che entra su una transizione t ha un numero di marche M uguale o superiore al numero di archi in entrata sulla transizione Pre(*,t). La condizione di abilitazione per ogni posto è $$ M \ge Pre(*,t) $$

Dove M è il numero di marche del posto che entra nella transizione, mentre Pre(*,t) è il numero di archi in entrata nella transizione.

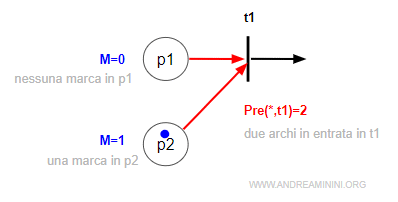
Una transizione abilitata si indica con il simbolo

$$ M[t> $$

Una transizione non abilitata, invece, si indica con il simbolo

$$ ¬ M[t> $$

Un esempio pratico

In questa rete di Petri le transizioni t₁ e t₂ sono abilitate.

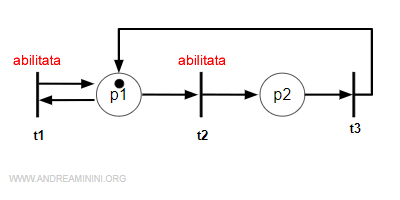
Spiegazione. La transizione t₁ ha un arco in ingresso Pre(*,t₁)=1 e il posto p₁ ha una marcatura M=1. Anche la transizione t₂ ha un arco in ingresso Pre(*,t₂)=1 e il posto p₁ ha una marcatura M=1. Viceversa, la transizione t₃ non è abilitata perché ha una transizione in ingresso Pre(*,t₃)=1 ma il posto p₂ ha zero marche M=0.

Anche in questa rete sono abilitate le transizioni t₂ e t₃.

Non è invece abilitata la transizione t₄ perché ha due archi in ingresso Pre(*,t₄)=2 e nessun posto in entrata (p₂, p₃) soddisfa la condizione M≥2

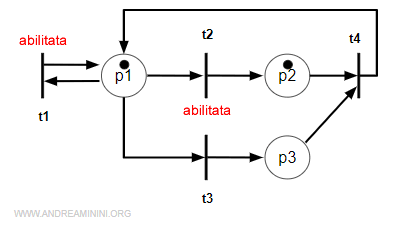
Nota. La transizione t₄ è abilitata soltanto se ogni posto in ingresso (p₂, p₃) soddisfa la condizione M≥2. Non basta che sia soddisfatta da un solo posto.

Il caso della transizione sorgente

Una transizione sorgente non ha archi in entrata.

$$ Pre(*,t)=0 $$

Pertanto, la transizione sorgente è sempre abilitata perché

$$ M \ge Pre(*,t)=0 $$

Esempio. In questa rete le transizioni abilitate sono t₁ e t₄. La transizione t₁ è una transizione sorgente senza archi in entrata Pre(*,t₁)=0. Pertanto, la condizione di abilitazione è soddisfatta M≥Pre(*,t₁) perché M=0 e Pre(*,t₁)=0. Quindi M≥0.

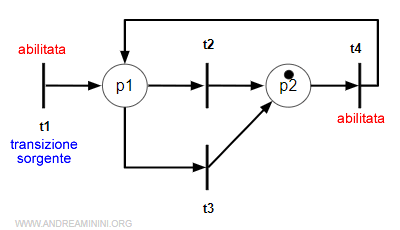
E così via