Algoritmo per trovare i P-invarianti della rete di Petri
Un algoritmo per trovare i vettori P-invarianti di una rete marcata è il seguente:
- Una rete ha m posti e n transizioni
- Calcolo la matrice di incidenza della rete C. La matrice ha m righe e n colonne.
- Aggiungo alla matrice C una matrice identità Imxm con m righe e m colonne. $$ C | I_{mxm} $$
- Elaboro la colonna j=1
- Per ogni elemento nella colonna j verifico se è possibile annullarlo con una combinazione lineare.
- Calcolo le eventuali combinazioni lineari (senza le duplicazioni), aggiungo il risultato con un'ulteriore riga alla tabella, elimino le colonne usate nel calcolo e lascio invariate le altre righe.
- Quando non ci sono più combinazioni lineari da calcolare, elimino dalla tabella le righe con elementi non nulli nella colonna j.
- Passo alla colonna j+1 e torno al punto [4] fino all'ultima colonna della matrice di incidenza (j=n).
Il risultato finale è una matrice di incidenza con tutti i valori nulli.
I valori nelle righe della matrice identità identificano gli eventuali vettori P-invariabili della rete.
Nota. Per trovare i vettori T-invariabili posso usare lo stesso algoritmo, usando la trasposta della matrice di incidenza. In questo caso ogni riga identifica una transizione. $$ C^T | I_{mxm} $$
Un esempio pratico
Ho una rete marcata con 4 posti e 3 transizioni.
La matrice di incidenza C della rete è
$$ C = \begin{pmatrix} 1 & 0 & 1 \\ -2 & 0 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & 0 \end{pmatrix} $$
La matrice ha m=4 righe, una per ogni posto della rete.
Aggiungo una matrice identità mxm ossia 4x4
$$ \begin{pmatrix} 1 & 0 & 1 \\ -2 & 0 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} $$
Poi considero le due matrici come una tabella.
Per semplicità chiamo le righe della tabella con i nomi dei posti: p1,p2,p3,p4
$$ \begin{vmatrix} p_1 \\ p_2 \\ p_3 \\ p_4 \end{vmatrix} \begin{vmatrix} 1 & 0 & 1 \\ -2 & 0 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & 0 \end{vmatrix} \begin{vmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{vmatrix} $$
A questo punto posso cominciare a lavorare sulle colonne della matrice di incidenza, dalla prima (j=1) all'ultima (j=3).
Prima colonna
Comincio a lavorare sulla prima colonna della matrice per C per cercare di annullare i valori in colonna.
Il primo elemento della colonna si annulla con la combinazione lineare 2p1+p2.
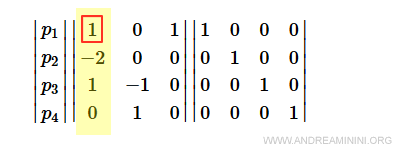
Il secondo elemento della colonna si annulla con le combinazioni lineari 2p1+p2 e 2p3+p2.
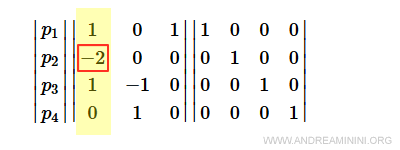
Il terzo elemento della colonna si annulla con l'operazione 2p3+p2.
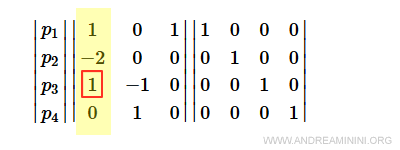
Le operazioni da compiere (senza considerare le ripetizioni sono) sono le seguenti combinazioni lineari: 2p1+p2 e 2p3+p2
Le aggiungo in fondo alla tabella
$$ \begin{vmatrix} p_1 \\ p_2 \\ p_3 \\ p_4 \\ 2p_1+p_2 \\ 2p_3+p_2 \end{vmatrix} \begin{vmatrix} 1 & 0 & 1 \\ -2 & 0 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \\ 0 & -2 & 0 \end{vmatrix} \begin{vmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 2 & 1 & 0 & 0 \\ 0 & 1 & 2 & 0 \end{vmatrix} $$
Poi elimino le righe p1,p2,p3 utilizzate nelle combinazioni lineari.
$$ \begin{vmatrix} p_4 \\ 2p_1+p_2 \\ 2p_3+p_2 \end{vmatrix} \begin{vmatrix} 0 & 1 & 0 \\ 0 & 0 & 2 \\ 0 & -2 & 0 \end{vmatrix} \begin{vmatrix} 0 & 0 & 0 & 1 \\ 2 & 1 & 0 & 0 \\ 0 & 1 & 2 & 0 \end{vmatrix} $$
Infine, elimino tutte le righe con valore non nullo nella prima colonna.
In questo caso non ci sono righe da eliminare.
Seconda colonna
Il primo elemento della seconda colonna si annulla con la combinazione lineare 2p4+(2p3+p2)
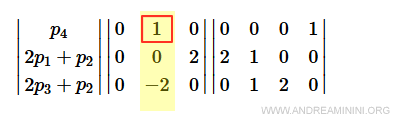
Il secondo elemento è nullo, quindi va bene così.
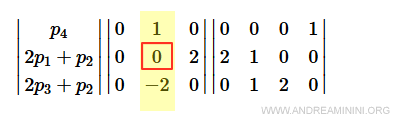
Il terzo elemento si annulla con la combinazione lineare 2p4+(2p3+p2)
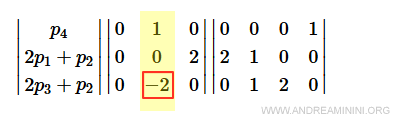
Pertanto, nella seconda colonna devo eseguire soltanto la combinazione linare 2p4+(2p3+p2)
La aggiungo in fondo alla tabella.
$$ \begin{vmatrix} p_4 \\ 2p_1+p_2 \\ 2p_3+p_2 \\ 2p_4+(2p_3+p_2) \end{vmatrix} \begin{vmatrix} 0 & 1 & 0 \\ 0 & 0 & 2 \\ 0 & -2 & 0 \\ 0 & 0 & 0 \end{vmatrix} \begin{vmatrix} 0 & 0 & 0 & 1 \\ 2 & 1 & 0 & 0 \\ 0 & 1 & 2 & 0 \\ 0 & 1 & 2 & 2 \end{vmatrix} $$
Poi elimino le righe p4 e (2p3+p2) usate nel calcolo.
$$ \begin{vmatrix} 2p_1+p_2 \\ 2p_4+(2p_3+p_2) \end{vmatrix} \begin{vmatrix} 0 & 0 & 2 \\ 0 & 0 & 0 \end{vmatrix} \begin{vmatrix} 2 & 1 & 0 & 0 \\ 0 & 1 & 2 & 2 \end{vmatrix} $$
Tutte le altre righe hanno valore nullo nella seconda colonna.
Quindi, non ci sono righe da annullare.
Terza colonna
Il primo elemento della terza colonna è non nullo (2).
Tuttavia, non ci sono combinazioni lineari possibili per eliminarlo.
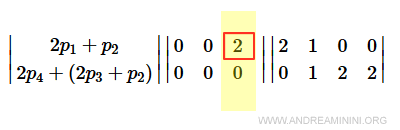
Il secondo elemento della terza colonna è nullo e va bene così.
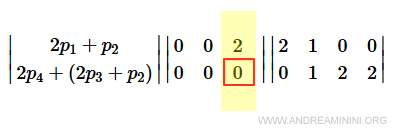
Pertanto, nella terza colonna non devo calcolare combinazioni lineari.
Devo soltanto eliminare le righe con valore non nullo in terza colonna.
In questo caso elimino la riga 2p1+p2.
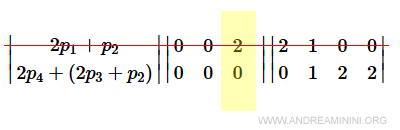
Il risultato finale
Le righe restanti nella tabella hanno valori nulli nella matrice di incidenza.
I valori nella matrice di identità sono i vettori P-invariabili della rete.
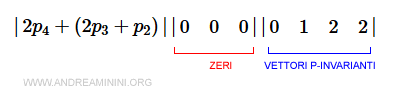
In questo caso c'è soltanto un vettore P-invariabile minimale, è il vettore x = [0 1 2 2]
$$ x = [ \: 0 \: 1 \: 2 \: 2 \: ] $$
Nota. Non è detto che ci sia sempre un solo vettore P-invariabile minimale. Potrebbe essercene più di uno oppure nessuno.
La verifica
Per ulteriore verifica moltiplico il vettore x per la matrice C.
$$ x \cdot C = [ \: 0 \: 1 \: 2 \: 2 \: ] \cdot \begin{pmatrix} 1 & 0 & 1 \\ -2 & 0 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & 0 \end{pmatrix} = [ \: 0 \: 0 \: 0 \: ] $$
Il risultato finale è un vettore nullo [ 0 0 0 ].
Pertanto, il vettore x è un vettore P-invariabile minimale.
Nota. Posso usare l'algoritmo anche per trovare i vettori crescenti, eliminando tutte le righe con elementi negativi. Allo stesso modo, posso usare l'algoritmo per trovare i vettori decrescenti eliminando tutte le righe con elementi positivi. Tuttavia, in questi casi l'algoritmo non si limita a trovare soltanto i vettori minimali e di supporto minimimo ma molti di più.
E così via.
