Marcatura raggiungibile nelle reti di Petri
In una rete marcata una marcatura M è detta marcatura raggiungibile se esiste una sequenza di scatto σ che permette di raggiungere M a partire da una marcatura iniziale M0. $$ M_0[σ>M $$
L'insieme delle marcature raggiungibili a partire da una marcatura iniziale M0 è detto insieme di raggiungibilità (R).
$$ R(N,M_0) $$
Può essere un insieme finito o infinito.
Un esempio pratico
Ho una rete di Petri con marcatura iniziale M0, due transizioni t1 e t2 e tre posti p0, p1, p2.
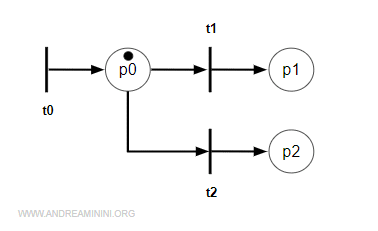
L'insieme di raggiungibilità da M0 è
$$ R(N,M_0) = \{ M_0, M_1, M_2 \} $$
ossia
$$ R(N,M_0) = \{ [1,0,0], [0,1,0], [0,0,1] \} $$
La marcatura M0=[1,0,0] si ottiene con una o più transizioni vuote ε.
Nota. Una transizione vuota ε non modifica la marcatura e lo stato della rete. E' comunque considerata una transizione abilitata. $$ M_0[ε>M_0 $$
La marcatura M1=[0,1,0] si verifica con la transizione t1.
La marcatura M2=[0,0,1] si verifica con la transizione t2.
Pertanto, il comportamento della rete a partire dalla marcatura M0 è
$$ L(N,M_0) = \{ e, t_1, t_2 \} $$
Nota. In questa rete non esiste una sequenza di transizioni che passi per tutte le marcature raggiungibili da M0. Ad esempio, se scatta la transizione t2 lo stato del sistema passa al posto p2. Da questo posto non può scattare la transizione t1. E viceversa.
E così via.
