Grafo di raggiungibilità della rete di Petri

Il grafo di raggiungibilità della rete di Petri è un grafo di una rete marcata <N,M₀> in cui ogni nodo è una marcatura raggiungibile e ogni arco è una transizione.

Nel grafo di raggiungibilità ogni marcatura raggiungibile è uno stato e appare una sola volta.

Le transizioni, invece, possono apparire più volte. Ogni transizione appare un numero di volte pari alle marcature che la abilitano.

A cosa serve il grafo di raggiungibilità

Il grafo di raggiungibilità rappresenta in modo sintetico tutte le sequenze di transizioni che possono scattare nella rete.

Inoltre, mostra a colpo d'occhio tutti gli stati raggiungibili del sistema (spazio degli stati) e le sequenze di transizioni che li determinano.

Attenzione. Il grafo di raggiungibilità è un'analisi esaustiva della rete di Petri perché prende in considerazione tutte le combinazioni possibili degli stati. Pertanto, se lo spazio di stato è infinito, anche il grafo di raggiungibilità è infinito.

Un esempio pratico

Questa rete marcata è composta da due marcature.

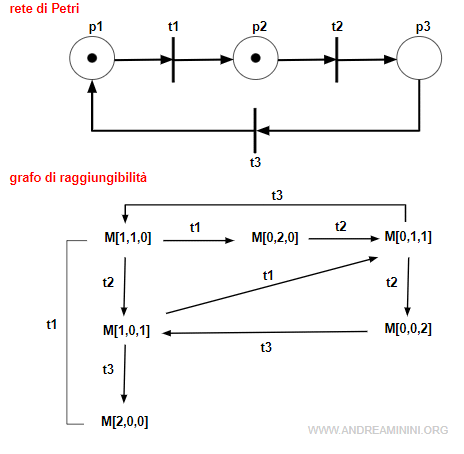
La marcatura iniziale è M[1,1,0].

In questo stato le transizioni abilitate sono t₁ e t₂ che dopo lo scatto possono condurre rispettivamente alle marcature [0,2,0] e [1,0,1]

Comincio a disegnare il grafo di raggiungibilità.

Nota. Per praticità coloro di rosso le nuove marcature. Le marcature già analizzate le coloro di nero per ricordarmi che non devo elaborarle di nuovo.

Ora analizzo la marcatura M[0,2,0].

In questo stato è abilitata soltanto la transizione t₂ che porta alla marcatura M[0,1,1].

La aggiungo al grafo di raggiungibilità.

Analizzo la marcatura M[1,0,1].

In questo stato le transizioni abilitate sono t₁ e t₃ che conducono rispettivamente alle marcature [0,1,1] e [2,0,0]

Aggiorno il grafo di raggiungibilità

Nota. Il nodo della marcatura [0,1,1] già esiste nel grafo di raggiungibilità. Quindi non va aggiunto. In questo caso è sufficiente collegare lo stato di partenza [1,0,1] allo stato di destinazione [0,1,1] tramite un arco.

Analizzo la marcatura M[0,1,1] in cui sono abilitate le transizioni t₂ e t₃ che conducono rispettivamente alle marcature [0,0,2] e [1,1,0]

Analizzo la marcatura M[2,0,0] in cui è abilitata solo la transizione t₁ che conduce alla marcatura [1,1,0]

Analizzo la marcatura M[0,0,2] in cui è abilitata solo la transizione t₃ che conduce alla marcatura [1,0,1]

A questo punto non ci sono altre marcature raggiungibili da analizzare.

Quindi, il grafo di raggiungibilità della rete è il seguente:

Nota. Come già anticipato il grafo di raggiungibilità rappresenta lo spazio degli stati della rete con le rispettive transizioni. Ogni singola marcatura (stato) appare una sola volta nel grafo mentre le transizioni possono comparire anche più volte.

Come costruire il grafo di raggiungibilità

A partire da una rete di Petri, con matrice di incidenza C, posso costruire il grafo di raggiungibilità seguendo questi passi.

1. Utilizzo la marcatura iniziale M₀ per disegnare il nodo radice del grafo.
2. Per ogni transizione abilitata da M $$ M \ge Pre(*,t) $$ calcolo la marcatura M'=M+C(*,t). Aggiungo il nodo M' al grafo (se non esiste già) e aggiungo un arco tra i nodi M e M'. A questo punto assegno un'etichetta (es. "ok" ) al nodo M per evitare di esaminarlo ulteriormente.
3. Ripeto le stesse operazioni del punto [2] per ogni altro nodo senza etichetta del grafo.

   Nota. L'algoritmo richiede un numero di iterazioni pari al numero delle marcature raggiungibili.

L'algoritmo termina quando tutti i nodi sono etichettati.

A questo punto, elimino tutte le etichette "ok" e il grafo di raggiungibilità è pronto.

Attenzione. Se lo spazio degli stati è infinito, l'algoritmo entra in un loop infinito.

E così via.