Analisi della rete con le equazioni di stato

L'analisi di una rete marcata <N,M₀> tramite le equazioni di stato mi permette di studiare la raggiungibilità di una marcatura tramite l'algebra lineare.

Questo consente di automatizzare l'analisi della raggiungibilità di una rete marcata.

Come funziona l'analisi dell'equazione di stato

Prendo in considerazione una generica rete marcata <N,M₀> con m posti e n transizioni.

L'equazione di stato studia la raggiungibilità di una marcatura M a partire dalla marcatura iniziale M₀

$$ M = M_0 + C \cdot σ $$

Dove C è la matrice di incidenza, ossia la differenza tra la matrice post e pre della rete.

La variabile sigma σ è la sequenza di transizioni che permette di raggiungere M da M₀.

$$ M_0[σ>M $$

Nota. Per un approfondimento sull'equazione di stato nella rete di Petri.

L'insieme potenzialmente raggiungibile Pr(N,M₀) è composto da tutte le marcature che soddisfano l'equazione di stato a partire dalla marcatura iniziale M0.

$$ PR(N,M_0) = \{ M \: | \: M=M_0+C \cdot k \} $$

Dove k è un vettore qualsiasi che soddisfa l'equazione di stato.

L'insieme di raggiungibilità R(N,M₀) della rete marcata è un sottoinsieme dell'insieme potenzialmente raggiungibile.

$$ R(N,M_0) \: ⊆ \: PR(N,M_0) $$

Dimostrazione. Se una marcatura M è raggiungibile, allora esiste una sequenza s tale che M₀[σ>M. Quindi, l'equazione di stato è soddisfatta con un vettore caratteristico k=σ. Non è detto però il contrario. Un vettore caratteristico k potrebbe non identificare una sequenza di transizioni σ abilitata dalla marcatura iniziale M₀ nella rete.

Le marcature potenzialmente raggiungibili ma non raggiungibili sono dette marcature spurie.

$$ PR(N,M_0) - R(N,M_0) $$

Un esempio pratico

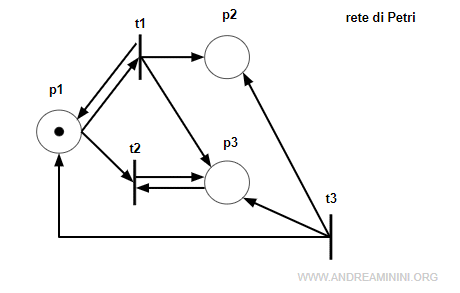
Questa rete marcata è formata da 3 posti e 3 transizioni.

Devo verificare se la marcatura M[1 1 1] è raggiungibile dalla marcatura iniziale M₀[1 0 0].

Per verificarlo uso la formula dell'equazione di stato da M₀ a M.

$$ M = M_0 + C \cdot k $$

$$ [1 \: 1 \: 1 ]^T = [1 \: 0 \: 0 ]^T + C \cdot k $$

Per calcolare la matrice di incidenza devo determinare le matrici pre e post della rete.

Essendoci 3 posti e 3 transizioni sono matrici quadrate 3x3.

$$ Pre = \begin{pmatrix} 1 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} $$

$$ Post = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \end{pmatrix} $$

Nota. Le matrici pre e post sono formate dalle transizioni (colonne) e dai posti (righe) della rete. La matrice pre conta gli archi in entrata nelle transizioni mentre la matrice post conta gli archi in uscita dalle transizioni.

La matrice di incidenza C della rete è la differenza delle matrici Post-Pre

$$ C = Post - Pre = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \end{pmatrix} - \begin{pmatrix} 1 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} $$

$$ C = Post - Pre = \begin{pmatrix} 0 & -1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \end{pmatrix} $$

Pertanto l'equazione di stato della rete è

$$ M = M_0 + C \cdot k $$

$$ [1 \: 1 \: 1 ]^T = [1 \: 0 \: 0 ]^T + \begin{pmatrix} 0 & -1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \end{pmatrix} \cdot k $$

A questo punto verifico se esiste un vettore k in grado di risolvere l'equazione.

$$ [1 \: 1 \: 1 ]^T - [1 \: 0 \: 0 ]^T = \begin{pmatrix} 0 & -1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \end{pmatrix} \cdot k $$

$$ [0 \: 1 \: 1 ]^T = \begin{pmatrix} 0 & -1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \end{pmatrix} \cdot k $$

$$ \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 & -1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} k_1 \\ k_2 \\ k_3 \end{pmatrix} $$

Nota. Per verificare se l'equazione vettoriale ha soluzioni, calcolo il prodotto tra la matrice e il vettore caratteritico k $$ \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 & -k_2 & k_3 \\ k_1 & 0 & k_3 \\ k_1 & 0 & k_3 \end{pmatrix} $$ Poi trasformo l'equazione vettoriale in un sistema di equazioni cartesiane o parametriche. $$ \begin{cases} 0 = -k_2 + k_3 \\ 1 = k_1 + k_2 \\ 1 = k_1 + k_2 \end{cases} $$ In questo modo posso cercare le soluzioni usando uno dei tanti metodi di risoluzione dell'algebra lineare. Ad esempio, il metodo della sostituzione.

L'equazione vettoriale si può risolvere con il vettore k = [ 0 1 1 ]

$$ [0 \: 1 \: 1 ]^T = \begin{pmatrix} 0 & -1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $$

Il vettore k = [ 0 1 1 ] appartiene all'insieme potenzialmente raggiungibile da Pr(N,M₀) ed equivale a dire che la marcatura M = [1 1 1] è raggiungibile con la sequenza di transizioni t₂t₃ o t₃t₂.

Tuttavia, queste sequenze non sono transizioni abilitate dalla marcatura M₀.

Quindi, le sequenze t₂t₃ o t₃t₂ non appartengono anche all'insieme di raggiungibilità R(N,M₀) della rete marcata.

Il vettore caratteristico k è soltanto una soluzione matematica al problema che non soddisfa anche i vincoli della rete.

In conclusione, la marcatatura M=[1 1 1] non è raggiungibile da M₀ ed è una marcatura spuria.

Nota. Questo accade perché l'analisi con le equazioni di stato soddisfa solo le condizioni necessarie per la raggiungibilità ma non quelle sufficienti.

I limiti dell'analisi con le equazioni di stato

Uno dei limiti di questa analisi è che identifica le condizioni necessarie e sufficienti per la raggiungibilità solo in determinate tipologie di reti marcate.

In generale, l'analisi tramite le equazioni di stato fornisce soltanto le condizioni necessarie ma non sufficienti per la raggiungibilità di una rete.

Nota. Le equazioni di stato sono condizioni necessarie e sufficienti per stabilire la raggiungibilità nelle macchine di stato, reti acicliche, grafi marcati.

Può comunque essere un'analisi preliminare per verificare se una marcatura è potenzialmente raggiungibile.

• Se una marcatura non è potenzialmente raggiungibile, allora è sicuramente non raggiungibile.
• Se una marcatura è potenzialmente raggiungibile, potrebbe essere raggiungibile oppure no. In questo caso, per confermarlo devo trovare almeno una sequenza di scatto σ abilitata da M₀ uguale al vettore caratteristico k.

  Nota. Soltanto nelle reti acicliche l'insieme di raggiungibilità R(N,M₀) coincide sempre con l'insieme potenzialmente raggiungibile PR(N,M₀).

Occorre però considerare che un'equazione di stato potrebbe essere soddisfatta da più vettori caratteristici y.

Quindi, se la raggiungibilità non è soddisfatta da un vettore k', potrebbe esserlo con un altro vettore k".

Nota. Questo vuol dire che se l'analisi di raggiungibilità non è soddisfatta dal vettore k, non si può affermare con certezza che la marcatura è spuria se il sistema di equazioni ha altre soluzioni. Devo verificarle tutte.

Se i vettori caratteristici k sono infiniti... ossia se il sistema di equazioni ha infinite soluzioni, l'analisi di raggiungibilità con le equazioni di stato diventa un problema complesso.

E così via