Le sequenze di transizioni stazionarie, crescenti e decrescenti

Una sequenza di transizioni σ in una rete marcata <N,M₀> può essere


• sequenza stazionaria
  se k·σ ⇔ M=M₀
• sequenza crescente
  se k·σ ⇔ M≥M₀
• sequenza decrescente
  se k·σ ⇔ M≤M₀.

Detto in altri termini, se ripeto una sequenza di transizioni s per k volte, la sequenza è stazionaria se la marcatura finale M è uguale alla marcatura iniziale M₀.

$$ M_0[σ>M = M_0 $$

La sequenza è crescente se il numero delle marcature finale è maggiore di quelle iniziali M≥M₀.

$$ M_0[σ>M \ge M_0 $$

Viceversa, la marcatura è decrescente se M≤M₀.

$$ M_0[σ>M \le M_0 $$

Come capire se una sequenza è stazionaria, crescente o decrescente

Calcolo la matrice di incidenza C della rete.

Poi verifico quali sono i T-vettori (y) della matrice di incidenza.

$$ C \cdot y $$

A questo punto possono verificarsi le seguenti situazioni

• Se esiste un T-vettore invariante y_I, allora la sequenza corrispondente s al vettore y_I è una sequenza di transizioni stazionaria.
  $$ k \cdot (σ=y_I) \Leftrightarrow M=M_0 $$
• Se esiste un T-vettore crescente y_C, allora la sequenza corrispondente s al vettore y_C è una sequenza di transizioni crescente, ripetitiva e non invariante.
  $$ k \cdot (σ=y_C) \Leftrightarrow M \ge M_0 $$
• Se esiste un T-vettore decrescente y_D, allora la sequenza corrispondente s al vettore y_D è una sequenza di transizioni decrescente e non invariante.
  $$ k \cdot (σ=y_D) \Leftrightarrow M \le M_0 $$

Nota. Nel caso del T-vettore decrescente non si può dire che la sequenza sia ripetitiva perché la sequenza è limitata inferiormente. Le marcature si riducono con gli eventi. Quindi, arriverà un momento in cui non ci sono più marcature nella rete. Viceversa, se il T-vettore è crescente le marcature aumentano e non c'è un limite superiore al numero della marcature.

Ovviamente, in una rete di Petri possono esistere uno o più T-vettori invarianti, crescenti, decrescenti.

Un esempio pratico

Questa rete marcata <N,M₀> è composta da tre transizioni e due posti.

La marcatura iniziale è M₀ = [1 0].

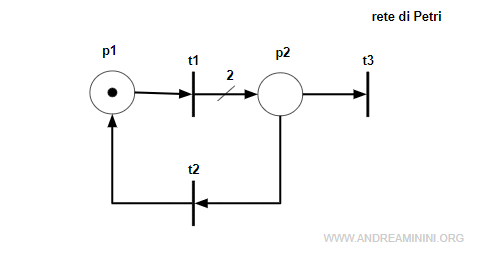
Calcolo la matrice di incidenza della rete tramite la differenza tra la matrice Post e Pre transizione.

$$ C = \begin{pmatrix} 0 & 1 & 0 \\ 2 & 0 & 0 \end{pmatrix} - \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \end{pmatrix} = $$

$$ C = \begin{pmatrix} -1 & 1 & 0 \\ 2 & -1 & -1 \end{pmatrix} $$

Esiste un vettore T invariante y_I=[1 1 1]^T tale che

$$ C \cdot y_I = 0 $$

$$ \begin{pmatrix} -1 & 1 & 0 \\ 2 & -1 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$

Il vettore y_I=[1 1 1] corrisponde a una sequenza di transizioni σ ottenuta combinando le transizioni t₁ t₂ e t₃

$$ σ = t_1 t_2 t_3 \\ σ = t_1 t_3 t_2 \\ σ = t_2 t_1 t_3 \\ σ = t_2 t_3 t_1 \\ σ = t_3 t_1 t_2 \\ σ = t_3 t_2 t_1 $$

La sequenza di transizione σ=t₁t₂t₃ è una sequenza stazionaria perché il sistema torna alla marcatura iniziale.

$$ M(1,0)[t_1>M(0,2) $$

$$ M(0,2)[t_2>M(1,1) $$

$$ M(1,1)[t_3>M(1,0) $$

ossia

$$ M(1,0)[t_1t_2t_3 >M(1,0) $$

Se ripeto k volte la stessa sequenza σ=t₁t₂t₃ ottengo lo stesso risultato, il sistema torna sempre alla marcatura iniziale M₀

$$ M(1,0)[k \cdot σ >M(1,0) $$

Ecco il grafo di raggiungibilità della sequenza

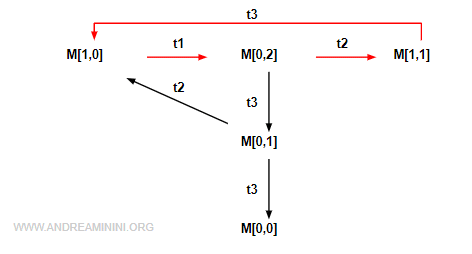
Nota. Anche la sequenza σ=t₁t₃t₂ è una sequenza stazionaria. $$ M(1,0)[t_1t_3t_2 >M(1,0) $$

E così via.