La rete di Petri etichettata
Una rete etichettata è una rete di Petri marcata <N,M0> con una funzione di etichetta l:T→ E che associa a ogni transizione t ∈ T un simbolo l(t) dell'alfabeto degli eventi e un insieme di marcature finali. $$ N_L = < N, M_0, l, F > $$
La funzione di etichetta mi permette di rappresentare una sequenza di scatto delle transizioni con un'unica parola w dell'alfabeto E.
I linguaggi di Petri
Nella rete di Petri alcune parole sono abilitate.
Queste ultime formano il linguaggio delle transizioni abilitate.
$$ L(N, M_0) $$
Il linguaggio generato è l'insieme delle parole (sequenze di scatto) abilitate dalla marcatura iniziale.
$$ L(N_l) $$
Il linguaggio accettato è l'insieme delle parole abilitate dalla marcatura iniziale che raggiungono una marcatura finale.
Un esempio pratico
Questa rete di Petri rappresenta un magazzino.
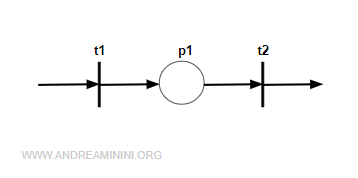
Per semplicità, il magazzino non ha una capacità massima e inizialmente è vuoto.
La rete ha due transizioni:
- La transizione t1 stocca un'unità di prodotto nel magazzino. Ogni volta che scatta, viene aggiunta una marca nel posto p1.
- La transizione t2 preleva un'unità di prodotto dal magazzino. La transizione è abilitata soltanto se il posto p1 ha almeno una marca.
La funzione di etichetta associa la lettera "a" alla transizione t1 e "b" alla transizione t2.
$$ l(t_1) = a \\ l(t_2) = b $$
Quindi l'alfabeto degli eventi E è
$$ E = \{ a, b \} $$
In questo esempio, la marcatura finale F è il magazzino vuoto.
Pertanto, il linguaggio generato è l'insieme delle parole w con un numero di simboli "a" maggiore di "b".
$$ aba \\ aab \\ aba \\ abaa \\ ababa \\ \vdots $$
Mentre, il linguaggio accettato è composto dall'insieme delle parole w con eguale numero di simboli "a" e "b".
$$ abab \\ aabb \\ abab \\ abaabb \\ ababab \\ \vdots $$
Linguaggi di Petri e automi
I linguaggi di Petri includono linguaggi regolari e irregolari.
Tutti i linguaggi regolari sono inclusi nei linguaggi di Petri.
Pertanto, qualsiasi automa può essere rappresentato con una rete di Petri associando ogni stato x a un posto della rete.
Viceversa, non è sempre possibile trasformare una rete di Petri in un'automa perché le RP includono anche i linguaggi regolari.
E così via.
