L'equazione di stato della rete di Petri
In una rete marcata <N,M0> l'equazione di stato determina la marcatura raggiungibile M a partire dalla marcatura iniziale M0 e dal vettore caratteristico di una sequenza di transizioni σ tramite la matrice di incidenza C della rete di Petri $$ M = M_0 + C \cdot σ $$
La dimostrazione
Ho una sequenza di transizioni σ
$$ σ = t_{k_1}, t_{k_2}, ... , t_{k_n} $$
La sequenza modifica la marcatura della rete
$$ M_0[σ>M_n $$
La prima transizione conduce alla marcatura M1
$$ M_0[t_{k_1}>M_1 $$
La seconda transizione conduce alla marcatura M2
$$ M_1[t_{k_2}>M_2 $$
E via dicendo fino alla marcatura Mn
$$ M_{n-1}[t_{n}>M_n $$
La prima marcatura posso riscriverla in questa forma
$$ M_1 = M_0 + C \cdot t_1 $$
E così la seconda fino alla n-esima marcatura
$$ M_2 = M_1 + C \cdot t_2 \\ M_3 = M_2 + C \cdot t_3 \\ \vdots \\ M_n = M_{n-1} + C \cdot t_n $$
Quindi, la marcatura dopo la sequenza delle n transizioni equivale alla sommatoria
$$ M_n = M_0 + \sum_{k=1}^n C \cdot t_{k} $$
ossia all'equazione di stato della rete marcata
$$ M_n = M_0 + C \cdot σ $$
Un esempio pratico
Ho una rete di Petri con marcatura iniziale M0 , tre posti e quattro transizioni
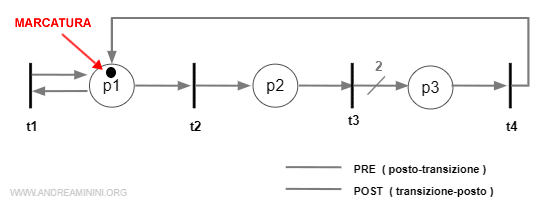
La marcatura iniziale è
$$ M_0 = [ 1 , 0 , 0 ] $$
La matrice di incidenza C è uguale alla differenza tra la matrice post e pre.
$$ C = Post - Pre = \begin{pmatrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \end{pmatrix} - \begin{pmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & -1 & 0 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 2 & -1 \end{pmatrix} $$
Analizzo la sequenza di transizione σ
$$ σ = t_1 t_1 t_2 t_3 $$
Nella sequenza la transizione t1 si verifica due volte, le transizioni t2 e t3 una volta e la transizione t4 zero volte.
Quindi il vettore caratteristico della sequenza è
$$ σ = [ 2, 1, 1, 0 ] $$
Calcolo l'equazione di stato in base a queste dati
$$ M = M_0 + C \cdot σ $$
$$ M = [ 1 , 0 , 0 ] + \begin{pmatrix} 0 & -1 & 0 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 2 & -1 \end{pmatrix} \cdot [ 2, 1, 1, 0 ] $$
Calcolo il prodotto riga per colonna tra la matrice C e il vettore σ.
$$ M = [ 1 , 0 , 0 ] + [ -1, 0, 2 ] $$
$$ M = [ 0 , 0 , 2 ] $$
E' la marcatura M dopo la sequenza di transizioni t1t1t2t3
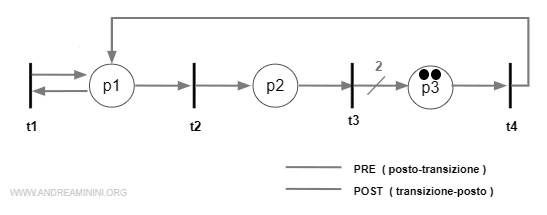
Nota. Nella marcatura finale ci sono due marche nel posto p3 perché la transizione t3 è composta da due archi verso p3.
E così via.
