L'elaborazione dati con le reti di Petri
Posso usare le reti di Petri anche per spiegare il flusso dei dati in un processo di elaborazione.
Un esempio pratico
Una calcolatrice scientifica deve calcolare un'espressione matematica.
$$ y = \frac{a^2}{a-b} $$
Le variabili in entrata (input) sono a e b mentre la variabile in uscita (output) è y.
L'espressione è composta da tre operazioni elementari.
- Divisione (x/z)
- Potenza (x·x)
- Sottrazione (x-z)
Nota. Dove x e z sono i valori in ingresso dell'operazione elementare. Da non confondere con le variabili a e b che invece sono i dati in input del circuito.
Nella rete di Petri ogni operazione è una transizione.
I posti della rete di Petri sono invece le locazioni di memoria dove sono registrati i valori delle variabili a, b, y durante il calcolo.
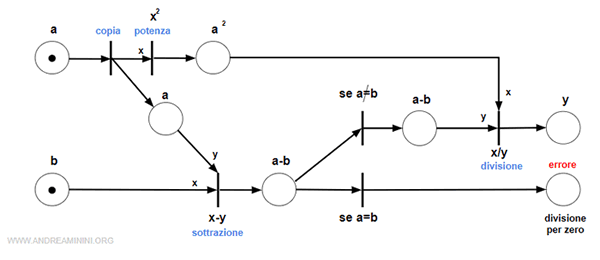
Alcune operazioni ( potenza e divisione ) sono svolte in sequenza.
Altre operazioni sono eseguite in parallelo ( potenza e sottrazione ) da due o più processori in struttura par begin.
La divisione è invece una struttura sincronizzata ( par end ) perché è vincolata al risultato delle operazioni precedenti.
Nota. Per svolgere il calcolo in parallelo ho dovuto aggiungere anche una funzione "copia" per copiare un dato in due locazioni di memoria. In questo modo, ogni processore lavora simultaneamente su una locazione diversa senza andare in conflitto con gli altri processori.
L'uscita del sistema dipende dalla sottrazione a-b.
- Se a-b=0 il denominatore è uguale a zero, la divisione non viene calcolata e il sistema restituisce un errore (divisione per zero).
- Se a-b≠0 il denominatore è diverso da zero, l'automa elabora la divisione e restituisce in output il risultato finale (y).
E così via.
