Le classi delle reti di Petri

Le reti di Petri P/T sono suddivise in diverse classi a seconda delle loro caratteristiche strutturali.

L'insieme che comprende tutte le classi è detto insieme delle reti generali.

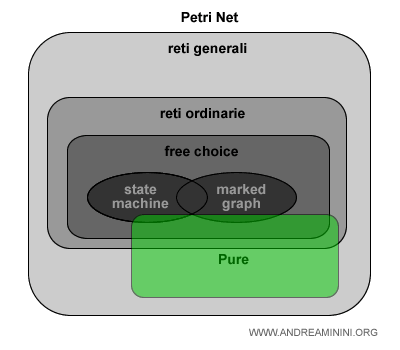
Le principali classi dell'insieme sono le reti ordinarie, a scelta libera (free choise), le macchine di stato (machine state), i grafi marcati (marked graph), le reti pure e ristrette.

Le reti ordinarie

Una rete è detta rete ordinaria se ogni arco della rete ha molteplicità unitaria.

La matrice Pre e Post di una rete ordinaria è composta esclusivamente dai numeri 0 e 1.

Esempio

Questa rete è ordinaria perché ogni arco ha un peso uguale a 1.

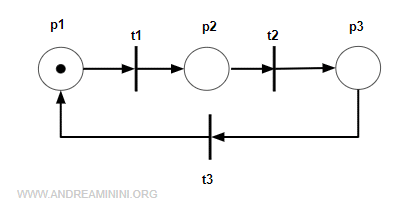
Le matrici pre e post della rete sono composte dai numeri 0 e 1.

$$ Pre(p,t) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

$$ Post(p,t) = \begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} $$

Nota. Se un arco in entrata o uscita da una transizione avesse avuto una molteplicità doppia sarebbe visibile il numero 2 rispettivamente nella matrice Pre o Post.

Le reti pure

Una rete è detta rete pura se la rete non contiene cappi.

Una rete è pura se il prodotto Pre(p,t)Post(p,t) per ogni transizione e posto è nullo.

$$ Pre(p,t) \cdot Post(p,t) = 0 $$

Esempio

Questa rete è pura perché non ha cappi

Date le matrici Pre e Post

$$ Pre(p,t) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

$$ Post(p,t) = \begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} $$

Il prodotto dei rispettivi elementi è nullo

$$ Pre(p_1, t_1) \cdot Post(p_1,t_1) = 1 \cdot 0 = 0 $$

$$ Pre(p_1, t_2) \cdot Post(p_1,t_2) = 0 \cdot 0 = 0 $$

$$ Pre(p_1, t_3) \cdot Post(p_1,t_3) = 0 \cdot 1 = 0 $$

$$ Pre(p_2, t_1) \cdot Post(p_2,t_1) = 0 \cdot 1 = 0 $$

$$ Pre(p_2, t_2) \cdot Post(p_2,t_2) = 1 \cdot 0 = 0 $$

$$ Pre(p_2, t_3) \cdot Post(p_2,t_3) = 0 \cdot 0 = 0 $$

$$ Pre(p_3, t_1) \cdot Post(p_3,t_1) = 0 \cdot 0 = 0 $$

$$ Pre(p_3, t_2) \cdot Post(p_3,t_2) = 0 \cdot 1 = 0 $$

$$ Pre(p_3, t_3) \cdot Post(p_3,t_3) = 1 \cdot 0 = 0 $$

Nota. Se fosse presente un cappio un prodotto avrebbe un elemento diverso da zero. Ad esempio, questa rete non è pura perché c'è un cappio tra p₁ e t₁.

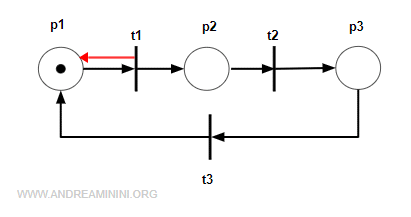
Il prodotto Pre(p₁,t₁)·Post(p₁,t₁) non è nullo. $$ Pre(p_1, t_1) \cdot Post(p_1,t_1) = 1 \cdot 1 = 1 \ne 0 $$

Le reti ristrette

Una rete è detta ristretta se è una rete ordinaria e pura.

Esempio

La rete dell'esempio precedente è una ristretta.

La rete è ordinaria perché i pesi degli archi sono tutti uguali a uno.

Nota. Gli archi uguali a zero sono gli archi assenti. Pertanto, appaiono nelle matrici Pre e Post ma non sono rappresentati nella rete.

Inoltre, è anche una rete pura perché non ci sono cappi.

Le macchine di stato

Una macchina di stato è una rete di Petri in cui ogni transizione ha un arco in entrata e in uscita.

Viceversa, i posti possono anche avere uno o più archi in entrata e/o uscita.

Ogni posto della macchina indica un particolare stato del sistema.

Esempio

Ecco un esempio di macchina di stato

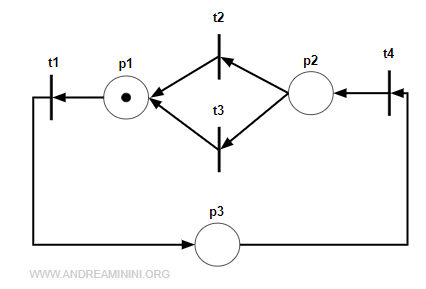
I grafi marcati

Un grafo marcato è una rete di Petri in cui ogni posto ha un arco in entrata e in uscita.

Viceversa, le transizioni possono anche avere uno o più archi in entrata e/o uscita.

Esempio

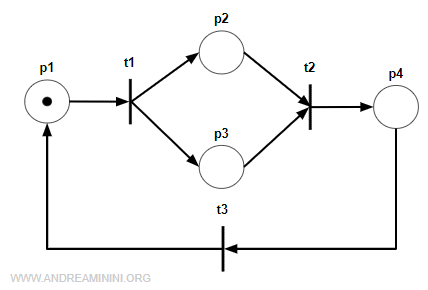
Ecco un esempio di grafo marcato.

Le reti a scelta libera

In una rete a scelta libera (free choise net) ogni arco tra un posto e una transizione è l'unico in uscita dal posto o l'unico in entrata nella transizione.

Le macchine di stato e i grafi marcati sono anche reti a scelta libera. Ma non è sempre detto il contrario.

Esempio

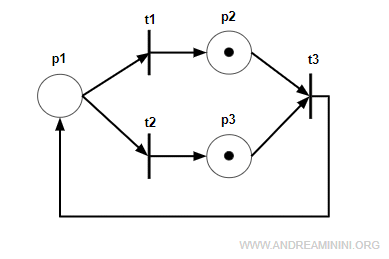
Ecco un esempio di rete a scelta libera.

E così via.