Albero di copertura delle reti di Petri
Cos'è l'albero di copertura?
L'albero di copertura è una rappresentazione di rete marcata (rete di Petri) in presenza di marcature duplicate.
A cosa serve?
La costruzione di un albero di copertura ha il vantaggio di terminare sempre in un numero finito di passi. Anche se nella rete ci sono dei loop che incrementano il numero delle marcature ( token ).
Nota. Per questa sua caratteristica l'albero di copertura è preferibile all'albero di raggiungibilità. In presenza di marcature crescenti, la costruzione dell'albero di raggiungibilità potrebbe entrare in un loop infinito.
Un esempio pratico
Ho una rete di Petri marcata <N,M0> con tre posti e due transizioni.
La marcatura iniziale M0 è M[1 0 0] poiché c'è un solo token (marca) nel posto p1.
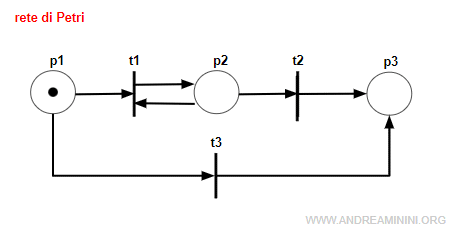
Nella rete è presente anche un ciclo che modifica il numero delle marcature, facendolo tendere all'infinito.
Questo rende impossibile la costruzione dell'albero di raggiungibilità perché le marcature diventano infinite.

Nota. Le marcature M[1 1 0] e M[1 2 0] non sono considerate duplicate nell'albero di raggiungibilità, perché il numero dei token è diverso. Quindi, l'algoritmo procede l'esecuzione all'infinito.
Per risolvere il problema costruisco l'albero di copertura.
Se il numero di token aumenta nella marcatura, invece di incrementare il contatore del posto inserisco il simbolo omega (ω).

Le ω-transizioni (omega transizioni) non sono elaborate dall'algoritmo.
Soltanto le posizioni con numeri naturali sono elaborate.
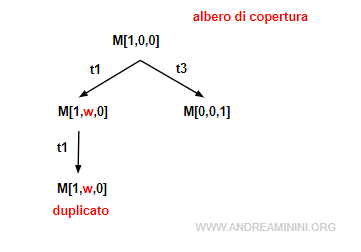
Esempio. Nella marcatura M[1,ω,0] l'algoritmo prende in considerazione la prima marca che abilita la transizione t1. Non prende in considerazione la seconda marca ω che abilita la transizione t3.
Questo escamotage mi permette di riconoscere tutte le marcature duplicate generate dal ciclo.
Nella struttura ad albero di copertura c'è un solo percorso tra il nodo radice e un altro nodo.

Così facendo la costruzione dell'albero termina in un numero finito di passi anche se l'insieme di raggiungibilità della rete marcata è infinito.
Nota. Nell'esempio precedente l'algoritmo costruisce l'albero di copertura, terminando l'esecuzione dopo soli 3 passi, ossia dopo tre scatti di transizione, perché la marcatura M[1,ω,0] è riconosciuta dall'algoritmo come duplicata.
E così via.
