Grafo marcato
Un grafo marcato è una rete ordinaria in cui ogni posto ha un arco in ingresso e un arco in uscita. $$ \sum_{t} Pre(p,t)= \sum_{t} Post(p,t)=1 $$ E' anche detto grafo di eventi.
In un grafo marcato ogni posto ha una sola transizione in uscita.
Le transizioni, invece, possono anche avere uno o più archi in entrata e/o in uscita.
Differenza tra macchina di stato e grafo marcato. In una macchina di stato accade esattamente l'inverso. Ogni transizione ha un solo arco in entrata e in uscita, mentre i posti possono avere uno o più archi in entrata e/o in uscita. Una rete può essere contemporaneamente sia una macchina di stato che un grafo marcato.
Un esempio di grafo marcato
Questa rete è un grafo marcato perché ogni nodo (p1,p2,p3) ha un solo arco in entrata e in uscita.
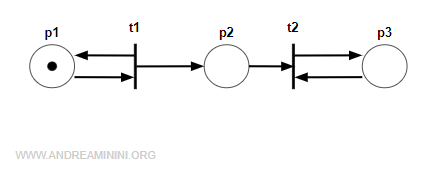
Le transizioni, invece, hanno uno o due archi in entrata e uscita.
Esempio 2
Anche questa rete è un grafo marcato.
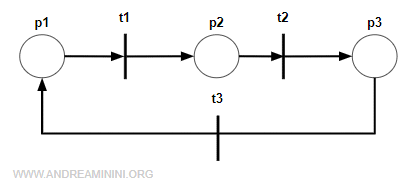
Tutti i posti hanno un arco in entrata e un arco in uscita.
Nota. Questa rete è anche una macchina di stato perché anche le transizioni hanno un solo arco in entrata e in uscita. A dimostrazione del fatto che una rete può essere contemporaneamente sia un grafo marcato che una macchina di stato.
Parallelismo e sincronizzazione nei grafi marcati
Pur avendo un solo arco in entrata e uscita in ogni posto, i grafi marcati consentono comunque sia il parallelismo che la sincronizzazione degli eventi perché le transizioni possono avere più archi in entrata e uscita.
Esempio
Questa rete è un grafo marcato
Grazie alla doppia uscita della transizione t1 permette il parallelismo del calcolo.
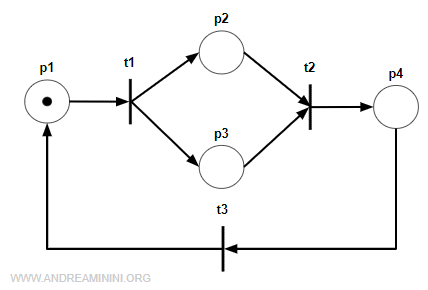
Inoltre, con la doppia entrata della transizione t2 permette anche la sincronizzazione del calcolo.
La dualità tra grafi marcati e macchine di stato
Un grafo marcato può essere trasformato in una macchina di stato sostituendo i posti con le transizioni e invertendo il verso degli archi.
Questo accade perché una macchina di stato è sempre una rete duale di un grafo marcato e viceversa.
Nota. Allo stesso modo una macchina di stato può essere trasformata in un grafo di stato seguendo la stessa procedura.
Un esempio pratico
Questa rete è un grafo marcato.

Nota. La matrice di incidenza del grafo marcato è $$ C = \begin{pmatrix} -1 & 0 & 1 \\ 1 & -1 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{pmatrix} $$
Sostituisco i posti con le transizioni. Poi inverto il verso degli archi.
Il risultato è una macchina di stato duale rispetto al grafo marcato primale.
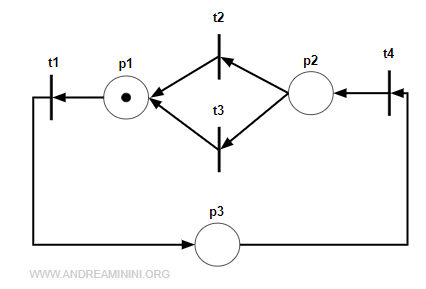
Nota. La matrice di incidenza del macchina di stato duale è uguale alla matrice trasposta della matrice di incidenza del grafo primale $$ C^T = \begin{pmatrix} -1 & 1 & 1 & 0 \\ 0 & -1 & -1 & 1 \\ 1 & 0 & 0 & -1 \end{pmatrix} $$
Teoremi e proprietà dei grafi marcati
Teorema 1
Dato un ciclo elementare orientato in un grafo marcato, un P-vettore composto da elementi pari a 1 nei posti del ciclo e 0 negli altri posti è un vettore P-invariante minimale di N.
Da notare, il ciclo deve essere "elementare" ossia non deve contenere al suo interno altri cicli.
Esempio
In questo grafo marcato c'è un ciclo elementare orientato p2t2p3t1.
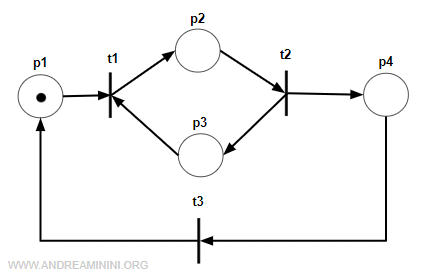
Il vettore caratteristico del ciclo elementare è x=[0 1 1 0] perché nel ciclo sono presenti i posti p2 e p3.
Il vettore x è un vettore P-invariante perché moltiplicato per la matrice di incidenza della rete dà come risultato un vettore nullo.
$$ x^T \cdot C $$
$$ [0 \: 1 \: 1 \: 0] \cdot \begin{pmatrix} -1 & 0 & 1 \\ 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 1 & -1 \end{pmatrix} = [0 \: 1 \: 1 \: 0] $$
Si tratta di un vettore P-invariante minimale perché non può essere ulteriormente ridotto, avendo tutti gli elementi positivi pari a 1.
Teorema 2
In un grafo marcato un T-vettore composto da tutti gli elementi uguali a 1 è T-invariante minimale.
Questo vuol dire che in un grafo marcato una sequenza di transizioni è stazionaria solo se contiene tutte le transizioni per lo stesso numero di volte.
Esempio
Questo grafo marcato è composto da 4 posti e 3 transizioni.

Il T-vettore composto da tutti uno y=[1 1 1] è un vettore T-invariante.
$$ C \cdot y $$
$$ \begin{pmatrix} -1 & 0 & 1 \\ 1 & -1 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$
E' anche un T-invariante minimale perché non può essere ulteriormente ridotto.
Teorema 3
Data una rete marcata M0, la rete <N,M0> del grafo marcato è una rete viva solo se assegna una marcatura a ogni ciclo elementare orientato.
Esempio
Questa rete è viva perché assegna una marcatura a ogni ciclo elementare orientato a partire da qualsiasi marcatura iniziale M0.
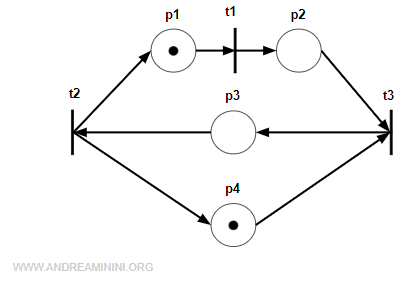
La rete ha due cicli orientati elementari p1t1p2t3p3t2 e p3t2p4t3.
Ogni ciclo orientato elementare ha un gettone (marcatura). Quindi la rete è viva.
Teorema 4
La rete <N,M0> di un grafo marcato è una rete reversibile soltanto se è una rete viva.
Esempio
Questo grafo marcato è una rete viva.

Quindi, è anche una rete reversibile
Teorema 5
La rete <N,M0> di un grafo marcato è una rete viva se per qualsiasi marcatura iniziale M0 l'insieme di raggiungibilità R eguaglia l'insieme potenzialmente raggiungibile PR e l'insieme X invariante Ix. $$ R(N,M_0) = PR(N,M_0) = I_x(N,M_0) $$
Questo teorema è uno strumento utile per studiare la raggiungibilità della rete nei grafi marcati, perché è una condizione necessaria e sufficiente per la raggiungibilità.
Esempio
Questo grafo marcato è composto da 4 posti e 3 transizioni.
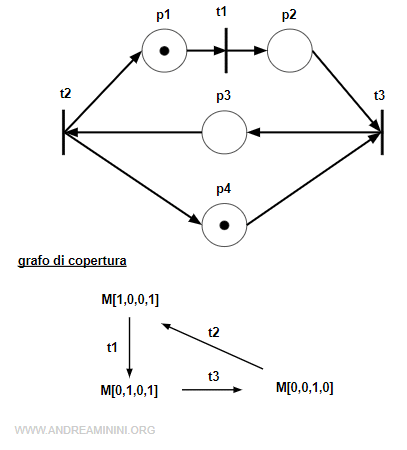
La marcatura iniziale M0 è
$$ M_0 = [ 1 \: 0 \: 0 \: 1 ] $$
La matrice di incidenza della rete è
$$ C = \begin{pmatrix} -1 & 1 & 0 \\ 1 & 0 & -1 \\ 0 & -1 & 1 \\ 0 & 1 & -1 \end{pmatrix} $$
La rete ha due cicli orientati elementari p1t1p2t3p3t2 e p3t2p4t3 con i rispettivi P-vettori caratteristici x'=[1 1 1 0] e x''=[0 0 1 1]. Sono entrambi vettori P-invarianti.
$$ x' \cdot C = [1 \: 1 \: 1 \: 0] \cdot \begin{pmatrix} -1 & 1 & 0 \\ 1 & 0 & -1 \\ 0 & -1 & 1 \\ 0 & 1 & -1 \end{pmatrix} = [0 \: 0 \: 0 ] $$
$$ x'' \cdot C = [0 \: 0 \: 1 \: 1] \cdot \begin{pmatrix} -1 & 1 & 0 \\ 1 & 0 & -1 \\ 0 & -1 & 1 \\ 0 & 1 & -1 \end{pmatrix} = [0 \: 0 \: 0 ] $$
Costruisco la matrice X dei cicli elementari mettendo i due vettori P-invarianti in colonna
$$ X = \begin{pmatrix} 1 & 0 \\ 1 & 0 \\ 1 & 1 \\ 0 & 1 \end{pmatrix} $$
Costruisco l'insieme X invariante a partire dai vettori P-invarianti.
$$ X^T \cdot M = X^T \cdot M_0 $$
Dove la marcatura iniziale M0=[1 0 0 1].
$$ X^T \cdot \begin{pmatrix} M(p_1) \\ M(p_2) \\ M(p_3) \\ M(p_4) \end{pmatrix} = X^T \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} $$
Mentre XT è la matrice trasposta composta dai vettori P-invarianti dei cicli elementari
$$ \begin{pmatrix} 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 \end{pmatrix} \cdot \begin{pmatrix} M(p_1) \\ M(p_2) \\ M(p_3) \\ M(p_4) \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} $$
Pertanto, l'insieme X-invariante è composto dalle soluzioni del seguente sistema vettoriale:
$$ \begin{pmatrix} M(p_1) & M(p_2) & M(p_3) & 0 \\ 0 & 0 & M(p_3) & M(p_4) \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$
ossia
$$ \begin{cases} M(p_1) + M(p_2) + M(p_3) = 1 \\ M(p_3) + M(p_4) = 1 \end{cases} $$
Pertanto, l'insieme X-invariante è composto dalle seguenti marcature:
$$ I_x = \{ \: [1 \: 0 \: 0 \: 1] \: , \: [0 \: 1 \: 0 \: 1] \: ] \: , \: [0 \: 0 \: 1 \: 0] \: \} $$
Essendo un grafo marcato l'insieme X-invariante coincide con l'insieme delle marcatura raggiungibili R (e potenzialmente raggiungibili PR).
$$ R = \{ \: [1 \: 0 \: 0 \: 1] \: , \: [0 \: 1 \: 0 \: 1] \: ] \: , \: [0 \: 0 \: 1 \: 0] \: \} $$
Nota. In effetti l'insieme X invariante coincide con le marcature del grafo di copertura della rete. Pertanto Ix=R.
Teorema 6
Un grafo marcato vivo è limitato se e solo se è strettamente connesso.
Teorema 7
Un grafo marcato vivo è strutturalamente limitato se e solo se è strettamente connesso.
E così via.
