Macchina di stato

Una macchina di stato è una rete ordinaria in cui ogni transizione ha un arco in entrata e in uscita. $$ \sum_{p} Pre(p,t)= \sum_{p} Post(p,t)=1 $$ E' anche detta grafo di stato.

Viceversa, i posti possono anche avere uno o più archi in entrata e/o uscita.

In una macchina di stato ogni posto della rete di Petri indica un particolare stato del sistema.

La marcatura iniziale della macchina di stato può basarsi su una o più marche.

Nota. Se la macchina di stato ha una sola marca è simile a un automa finito.

Un esempio pratico

Questa rete di Petri è una macchina di stato perché ogni posto ha un arco in entrata e in uscita.

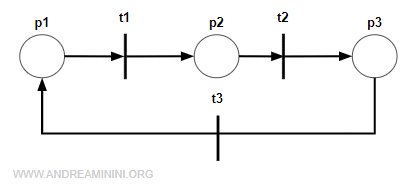
Nota. L'arco in entrata e in uscita dallo stesso posto possono anche essere collegati a una stessa transizione. Pertanto, la macchina di stato ammette anche la presenza di cappi al suo interno. Detto in altri termini, una macchina di stato può essere o meno una rete pura.

La matrice di incidenza della macchina di stato

La matrice di incidenza di una macchina di stato è composta da vettori colonna con un elemento pari a 1 (arco in uscita) e un elemento pari a -1 (arco in entrata) oppure con tutti gli elementi pari a zero se in presenza di un cappio.

Esempio

Questa rete è una macchina di stato

la sua matrice di incidenza è

$$ C = \begin{pmatrix} -1 & 0 & 1 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{pmatrix} $$

In questo caso ogni vettore colonna è composto da un elemento +1 e un elemento -1.

Parallelismo e sincronizzazione nelle macchine di stato

Le macchine di stato consentono il parallelismo degli eventi perché i posti possono avere più archi in uscita.

Non consentono, invece, la sincronizzazione perché le transizioni possono avere un solo arco in entrata.

Esempio

Ecco un esempio pratico di macchina di stato che realizza il parallelismo del calcolo.

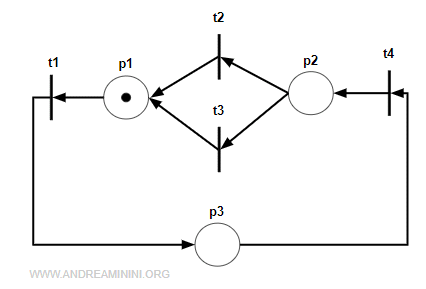
La doppia uscita dal posto p₂ realizza il parallelismo.

Il doppio ingresso nel posto p₁ invece non realizza la sincronizzazione.

Teoremi sulle macchine di stato

Teorema 1

Una macchina di stato è una rete limitata e strettamente conservativa.

Una rete è strettamente conservativa se il numero delle marcature è costante.

Se la rete è strettamente conservativa allora il vettore composto da tutti gli elementi pari a 1 è un vettore P-invariante minimale per la rete.

Esempio

$$ 1^T \cdot C $$

$$ [1 \: 1\: 1] \cdot \begin{pmatrix} -1 & 0 & 1 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{pmatrix} = [0 \: 0 \: 0] $$

Pertanto, il vettore 1^T è un vettore P-invariante.

E' anche un vettore P-invariante minimale perché non esiste nessun vettore P-invariante inferiore.

Dimostrazione. Se per ipotesi esistesse un vettore P-invariante x inferiore al vettore [1 1 1] (ad esempio x=[1 1 0]) con un supporto P'=||x|| non ci sarebbe alcuna connessione con i restanti posti della rete P\P'. Se fossero connessi ci sarebbe una transizione in entrata o in uscita da uno dei posti P\P'. In questo caso però il prodotto con la colonna di incidenza sarebbe pari a 1 o -1 e il vettore x non sarebbe P-invariante. Quindi, è impossibile.

Esempio. Data la seguente rete

Se il vettore x=[1 1 0] fosse P-invariante minimale avrebbe un insieme supporto ||x||={p₁,p₂}=P' e non avrebbe alcuna connessione con P/P'={p₃}. $$ [1 \: 1\: 0] \cdot \begin{pmatrix} -1 & 0 & 1 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{pmatrix} = [0 \: -1 \: 1] $$ L'unico modo per avere un vettore P-invariante con x=[1 1 0] si ottiene modificando la matrice di incidenza $$ [1 \: 1\: 0] \cdot \begin{pmatrix} -1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & -1 \end{pmatrix} = [0 \: 0 \: 0] $$ Così facendo però la struttura della rete sarebbe diversa con la sottorete {P₁,P₂} non connessa a {P₃}

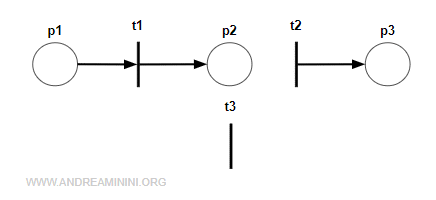
Pertanto non esiste nessun vettore P-invariante minimale inferiore al vettore 1^T=[1 1 1].

Teorema 2

Dato l'insieme I = {c₁,c₂,...,c_r} dei cicli elementari orientati della rete N, il vettore caratteristico y di ogni ciclo è un vettore T-invariante minimale della rete.

Da notare, il teorema parla di cicli orientati "elementari" ossia quelli che non contengono all'interno altri cicli orientati.

Quindi, non vanno presi in considerazione tutti i cicli orientati.

Esempio

Ho una rete con tre posti e quattro transizioni.

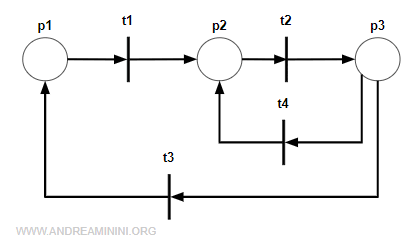
La rete ha due cicli orientati elementari c₁ = t₁t₂t₃ e c₂ = t₂t₄

$$ I = \{ c_1, c_2 \} $$

Il vettore caratteristico del ciclo c₁= t₁t₂t₃ è

$$ y_1 = [1 \: 1 \: 1 \: 0] $$

Moltiplico la matrice di incidenza della rete per il vettore y₁

$$ \begin{pmatrix} -1 & 0 & 1 & 0 \\ 1 & -1 & 0 & 1 \\ 0 & 1 & -1 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$

Quindi il vettore caratteristico y₁ è un vettore T-invariante.

Essendo un ciclo orientato elementare il vettore y è anche T-invariante minimale perché non esiste un vettore inferiore.

Ora analizzo il secondo ciclo c₂= t₂t₄ il cui vettore caratteristico è

$$ y_2 = [0 \: 1 \: 0 \: 1] $$

Moltiplico la matrice di incidenza della rete per il vettore y₂

$$ \begin{pmatrix} -1 & 0 & 1 & 0 \\ 1 & -1 & 0 & 1 \\ 0 & 1 & -1 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$

Anche il vettore caratteristico y₂ è un vettore T-invariante ed è minimale perché si tratta di un ciclo elementare.

Teorema 3

Per qualunque marcatura iniziale M₀ la rete <N,M₀> è una rete reversibile solo se i posti marcati da M₀ sono assorbenti.

Un posto è assorbente se riceve archi in entrata.

Nota. La dimostrazione è banale. Se il posto iniziale non fosse assorbente la marca potrebbe solo uscire e una volta uscita non potrebbe più tornarvi. In tale caso la rete non può essere reversibile.

Teorema 4

Per qualunque marcatura iniziale M₀ la rete <N,M₀> è una rete viva se e solo se nella marcatura iniziale M₀ c'è almeno una marca e la rete è fortemente connessa.

• Una rete è viva se qualsiasi transizione può essere abilitata da qualsiasi marcatura iniziale tramite un'opportuna sequenza di transizioni.
• Una rete è fortemente connessa se per ogni coppia di posti (p_j,p_k) esiste un cammino orientato.

Esempio

Questa rete è fortemente connessa perché ogni coppia di posti c'è un cammino orientato ossia una sequenza di transizioni che permette di collegarli (p_j,p_k).

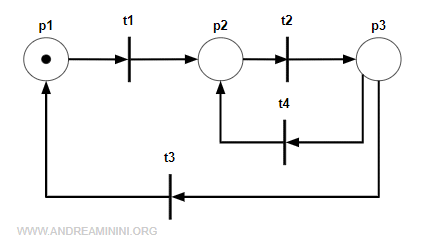
Ad esempio la coppia di posti (p₁,p₃) è connessa dalla sequenza di transizioni σ=t₁t₂ ed esiste almeno un cammino orientato inverso σ=t₃ che permette di collegare la coppia (p₃,p₁).

Lo stesso vale per qualsiasi altra coppia di posti.

Quindi la marca presente in M₀ può abilitare tutte le transizioni della rete perché la marca può spostarsi in tutti i posti della rete.

Esempio. La marcatura iniziale M₀=[1 0 0] abilita tutte le transizioni. Abilita t₁ direttamente, abilita t₂ con la sequenza σ=t₁. Abilita t₃ e t₄ con la sequenza σ=t₁t₂.

Allo stesso modo qualsiasi altra marcatura iniziale ( M₀=[0 1 0] e M₀=[0 0 1] ) abilita tutte le transizioni della rete.

Esempio. La marcatura M₀=[0 1 0] abilita tutte le transizioni. Abilita t₂ direttamente. Abilita t₃ e t₄ con la sequenza σ=t₂. Abilita t₁ con la sequenza σ=t₂t_3.

Pertanto, la rete è viva.

Nota. Se non ci fossero marche iniziali non sarebbe possibile far scattare alcuna transizione. La rete sarebbe bloccata, pertanto morta. Inoltre, se la rete non fosse strettamente connessa ci sarebbero transizioni quasi vive o morte in alcune marcature iniziali. In tali casi la rete non può essere definita viva.

Teorema 5

Per qualunque marcatura iniziale M₀ della rete <N,M₀> l'insieme delle marcature raggiungibili R è uguale all'insieme potenzialmente raggiungibile $$ R(N,M_0) = PR(N,M_0) $$

In genere, in una rete P/T ogni marcatura raggiungibile è sempre potenzialmente raggiungibile ma non vale l'inverso.

$$ R(N,M_0) ⊆ PR(N,M_0) $$

Nelle macchine di stato questa relazione è biunivoca. Ogni marcatura potenzialmente raggiungibile è anche raggiungibile.

Dimostrazione

Una marcatura potenzialmente raggiungibile M è raggiungibile dalla marcatura iniziale M₀ se esiste un vettore y tale che

$$ M = M_0 + C \cdot y $$

Esempio. In questa rete la marcatura iniziale è M₀=[1 0 0]. Le marcature potenzialmente raggiungibili PR con lo stesso numero di marche sono M[1 0 0] , M[0 1 0] e M[0 0 1].

Per la marcatura M[0 0 1] esiste un vettore y tale che $$ M = M_ 0 + \begin{pmatrix} -1 & 0 & 1 & 0 \\ 1 & -1 & 0 & 1 \\ 0 & 1 & -1 & -1 \end{pmatrix} \cdot \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix} $$ Quindi il vettore y=[1 1 0 0]. $$ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} -1 & 0 & 1 & 0 \\ 1 & -1 & 0 & 1 \\ 0 & 1 & -1 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \\ 0 \end{pmatrix} $$ Il vettore y indica l'insieme (ma non la sequenza) delle transizioni per raggiungere M da M₀.

Qualsiasi marcatura M diversa da M₀ è raggiungibile tramite un'opportuna sequenza di transizioni.

Sapendo che nelle macchine di stato il vettore 1^T è P-invariante, la marcatura M e M₀ hanno lo stesso numero di marche.

$$ 1^T \cdot M = 1^T \cdot M_0 $$

Quindi le marcature potenzialmente raggiungibili della macchina di stato devono avere una marca.

$$ PR = \{ M[1,0,0] \: M[0,1,0] \: M[0,0,1] \} $$

Devo verificare se sono tutte raggiungibili a partire da una marcatura iniziale M₀.

Prendo in considerazione una generica marcatura M di PR(N,M₀).

Essendo due marcature diverse M≠M₀ deve esistere almeno un posto p in cui le due marche si distinguono.

$$ 0 \le M(p) < M_0(p) $$

Pertanto, se M(p)<M₀(p) allora la differenza M(p)-M₀(p) è negativa

$$ M(p)-M_0(p)<0 $$

Esempio. Confrontando le marcature M₀=[1 0 0] e M[0 0 1] si nota subito che soltanto con il posto p₁ si soddisfa la disequazione $$ 0 \le M(p_1) < M_0(p_1) $$ dove M(p₁)=0 e M₀(p₁)=1. Quindi la differenza tra le marcature M(p₁)-M₀(p₁) è negativa $$ M(p_1) - M_0(p) = 0 - 1 < 0 $$

Se la differenza M(p)-M₀(p) è negativa, vuol dire che esiste un vettore y tale che

$$ C(p,*) \cdot y < 0 $$

Gli elementi positivi del vettore y indicano le transizioni della rete che hanno il posto p in ingresso.

Esempio. Se M(p₁)-M₀(p₁)<0 prelevo dalla matrice di incidenza la riga del posto p₁ rispetto a tutte le transizioni. $$ C(p_1,*) = ( -1 \: 0 \: 1 \: 0 ) $$ Verifico se esiste un vettore y tale che $$ C(p_1,*) \cdot y < 0 $$ Questo vettore è y=[1 0 0 0] $$ ( -1 \: 0 \: 1 \: 0 ) \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} < 0 $$ L'elemento positivo del vettore y indica la transizione abilitata che ha per ingresso il posto p₁. In questo caso si tratta della transizione t₁.

Avendo il posto p una marca le transizioni sono abilitate e possono scattare.

Si passa così dalla marcatura iniziale M₀ a una nuova marcatura M'.

Esempio. La transizione t₁ scatta portando la rete dalla marcatura M₀[1 0 0] alla marcatura M'=[0 1 0].

A questo punto il procedimento si ripete daccapo sostituendo M₀ con M'.

Essendo due marcature diverse M'≠M₀ c'è almeno un posto p in cui le due marche si distinguono.

$$ 0 \le M(p) < M'(p) $$

Pertanto, se M(p)<M'(p) allora la differenza M(p)-M'(p) è negativa

$$ M(p)-M'(p)<0 $$

Esempio. Confrontando le marcature M'=[0 1 0] e M[0 0 1] si nota subito che soltanto con il posto p₂ si soddisfa la disequazione $$ 0 \le M(p_2) < M'(p_2) $$ dove M(p₂)=0 e M'(p₂)=1. Quindi la differenza tra le marcature M(p₂)-M'(p₂) è negativa $$ M(p_2) - M'(p) = 0 - 1 < 0 $$

Se la differenza M(p)-M'(p) è negativa, vuol dire che esiste un vettore y tale che

$$ C(p,*) \cdot y < 0 $$

Gli elementi positivi del vettore y indicano le transizioni della rete che hanno il posto p in ingresso.

Esempio. Se M(p₂)-M'(p₂)<0 prelevo dalla matrice di incidenza la riga del posto p₂ rispetto a tutte le transizioni. $$ C(p_2,*) = ( 1 \: -1 \: 0 \: 1 ) $$ Verifico se esiste un vettore y tale che $$ C(p_2,*) \cdot y < 0 $$ Questo vettore è y=[0 1 0 0] $$ ( 1 \: -1 \: 0 \: 1 ) \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} < 0 $$ L'elemento positivo del vettore y indica la transizione abilitata che ha per ingresso il posto p₂. In questo caso si tratta della transizione t₂.

Avendo il posto p una marca le transizioni sono abilitate e possono scattare.

Si passa così dalla marcatura iniziale M' a una nuova marcatura M".

Esempio. La transizione t₂ scatta portando la rete dalla marcatura M'[0 1 0] alla marcatura M"=[0 0 1].

La nuova marcatura M'' coincide con la marcatura M che volevo raggiungere. Quindi la marcatura M è raggiungibile.

Il processo termina quando la nuova marcatura M"=M

E così via.