Lo scatto di una transizione nella rete di Petri
Nella rete di Petri una transizione abilitata da una marcatura M può scattare. Lo scatto di una transizione t consiste in una nuova marcatura M' che sostituisce la marcatura precedente. $$ M'=M-Pre(*,t)+Post(*,t) \\ =M+C(*,t) $$
Lo scatto elimina la transizione dal vettore M e la aggiunge al vettore M'.
Lo scatto della transizione è indicato con il simbolo
$$ M[t>M' $$
Nota. Il simbolo C è la differenza algebrica tra le matrici Post e Pre. $$ C = Post - Pre $$
Un esempio pratico
In questa rete la transizione t2 è abilitata dalla marcatura nel posto p1
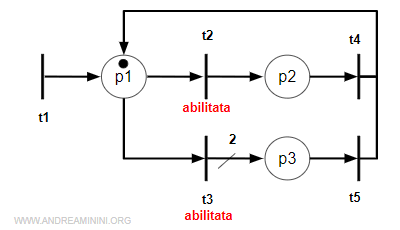
Quando scatta la transizione t2 la marca si sposta dal posto p1 al posto p2.
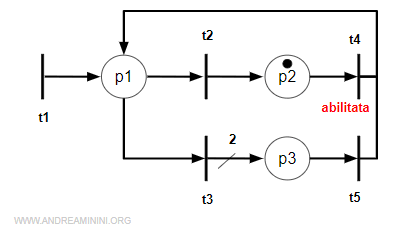
Adesso la transizione abilitata è la t4 perché la marca si trova nel posto p2.
$$ M'=M-Pre(*,t)+Post(*,t) = 1 - 1 + 1 = 1 $$
Nota. Se ora scattasse la transizione t1, t3, t5 o di nuovo t2 la situazione resterebbe immutata con la marca nel posto p2. La marcatura si sposta soltanto nel caso di uno scatto in una transizione abilitata. Questo però non esclude che possano anche scattare le altre transizioni non abilitate nel corso del tempo.
Quando scatta la transizione t4 la marca torna al posto p1.

A questo punto, cerco di capire cosa accade quando scatta la transizione t3.
Anche la transizione t3 è abilitata ma si congiunge con il posto p3 con due archi anziché 1.
$$ M'=M-Pre(*,t)+Post(*,t) = 1 - 1 + 2 = 2 $$
In questo caso lo scatto sposta la marca e la raddoppia nel posto p3.
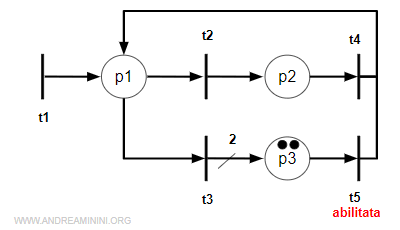
Quando scatta di nuovo la transizione t5 soltanto una marca si sposta nel posto p1 perché c'è solo un arco di collegamento.
L'altra marca resta nel posto p3.
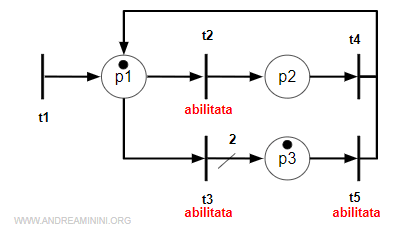
E così via.
