Reti di Petri acicliche
Le reti di Petri sono reti acicliche se non presentano dei cicli orientati.
L'equazione di stato di una rete aciclica non contiene marcature spurie.
Cos'è una marcatura spuria? Una marcatura spuria è una marcatura potenzialmente raggiungibile ma non raggiungibile.
Pertanto, in una rete aciclica l'insieme di raggiungibilità (R) coincide sempre con l'insieme potenzialmente raggiungibile (PR) data una marcatura iniziale M0
$$ R(N,M_0) = PR(N,M_0) $$
Nota. Nelle reti acicliche il problema della raggiungibilità si può risolvere con l'analisi dell'equazione di stato.
Un esempio di rete aciclica
Questa rete è una rete aciclica perché non contiene cicli orientati, né cappi.
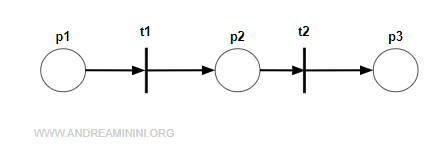
Anche questa rete è una rete aciclica.
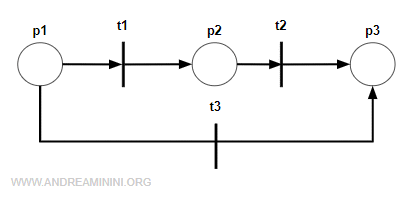
Viceversa, questa rete non è aciclica perché contiene un ciclo orientato.
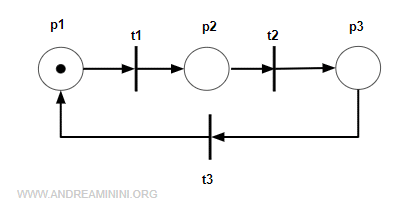
Anche questa rete non è aciclica perché contiene un cappio p2t2p2 che equivale a un ciclo orientato.
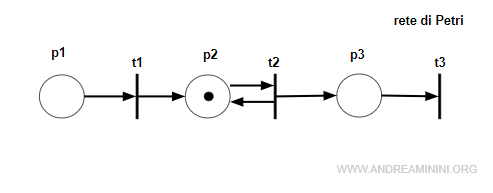
Le reti acicliche e le reti pure
Tutte le reti acicliche sono reti pure. Non è però detto che una rete pura sia anche aciclica.
Esempio
Questa rete è una rete pura perché non contiene cappi.

Tuttavia, la rete non è anche una rete aciclica perché contiene un ciclo p1t1p2t2p3t3 all'interno.
E così via.
