Albero di raggiungibilità della rete di Petri

L'albero di raggiungibilità è una rappresentazione della rete di Petri. E' alternativa al grafo di raggiungibilità.

A cosa serve?

E' utile per mettere in evidenza le marcature duplicate della rete.

Ecco un esempio pratico di albero di raggiungibilità

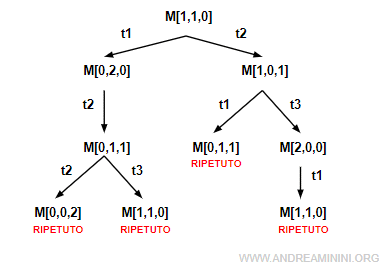
Come costruire un albero di raggiungibilità

A partire da una rete di Petri, costruisco il suo grafo di raggiungibilità.

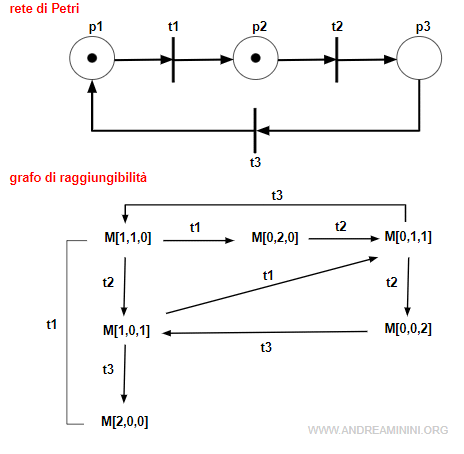
In questa forma non è facile vedere le marcature duplicate.

Quindi, costruisco l'albero di raggiungibilità.

Al vertice dell'albero metto la marcatura iniziale M[1,1,0].

Nota. La marcatura M[1,1,0] vuol dire che c'è una marca sia nel posto 1 che nel posto 2. Non c'è nessuna marca nel posto 3 della rete di Petri.

Da questa marcatura sono abilitate due transizioni t₁ e t₂ che conducono rispettivamente alle marcature M[0,2,0] e M[1,0,1].

Queste transizioni formano i rami dell'albero dal vertice a due nodi di livello inferiore che identificano le marcature M[0,2,0] e M[1,0,1].

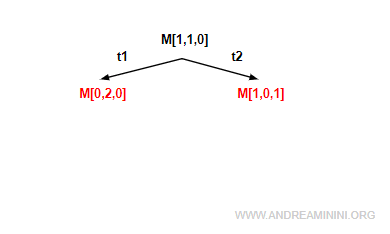
Scendo di livello e analizzo il nodo M[0,2,0] in cui è abilitata soltanto la marcatura t2 che conduce alla nuova marcatura M[0,1,1] di livello inferiore.

Poi analizzo l'altro nodo M[1,0,1] in cui sono abilitate le transizioni t1 e t3 che conducono alle marcature M[0,1,1] e M[2,0,0].

Quindi, aggiungo all'albero altri due rami e due nodi di livello inferiore.

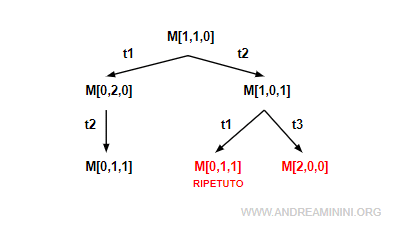
Nota. Poiché la marcatura M[0,1,1] è già presente nell'albero di raggiungibilità, al nodo M[0,1,1] aggiungo l'etichetta RIPETUTO. I rami con nodi duplicati diventano foglie ossia non hanno altri rami inferiori perché sarebbero duplicati nell'albero.

Ora analizzo la marcatura M[0,1,1] in cui sono abilitate le transizioni t2 e t3 che conducono alle marcature M[0,0,2] e M[1,0,1].

Sono entrambi nodi duplicati. Quindi, questi due rami diventano foglie.

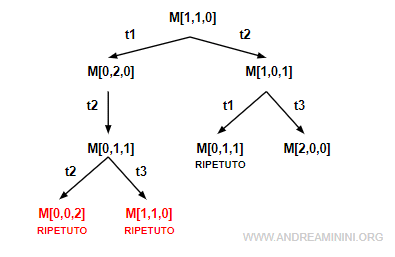
Infine, analizzo la marcatura M[2,0,0] in cui è abilitata soltanto la transizione t2 che conduce alla marcatura M[1,1,0].

Si tratta di un'altra marcatura già presente nell'albero quindi etichetto il nuovo nodo come "ripetuto".

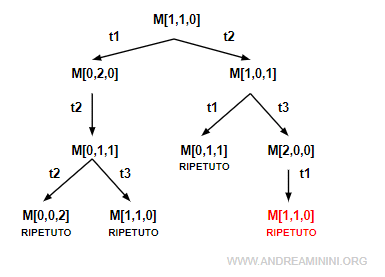
Non essendoci altre marcature da analizzare, la costruzione dell'albero di raggiungibilità si conclude qui.

Guardando l'albero di raggiungibilità è subito evidente constatare quali marcature sono ripetute nella rete di Petri.

E così via.