Vettore T invariante minimale
Cos'è un vettore T-invariante
Un vettore T-Invariante y è detto minimale se non esiste un altro vettore T-invariante y' tale che $$ y' < y $$
A cosa serve?
Ogni vettore T-invariante non minimale è determinato da una combinazione lineare con coefficienti interi di uno o più vettori T-invarianti minimali.
Nota. Un vettore T-invariante minimale può essere di supporto minimo oppure no.
Un esempio pratico
Prendo in considerazione una rete marcata con due posti e tre transizioni
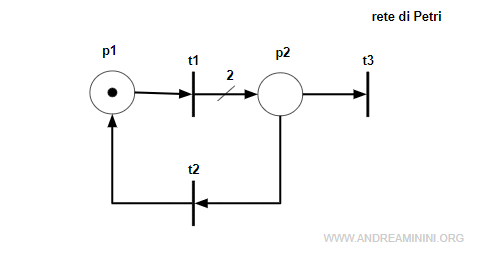
Calcolo la matrice di incidenza C della rete tramite la differenza tra la matrice Post e Pre transizione.
$$ C = \begin{pmatrix} 0 & 1 & 0 \\ 2 & 0 & 0 \end{pmatrix} - \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \end{pmatrix} = $$
$$ C = \begin{pmatrix} -1 & 1 & 0 \\ 2 & -1 & -1 \end{pmatrix} $$
Il vettore y = [1 1 1] è T-invariante perché
$$ C \cdot y_I = 0 $$
$$ \begin{pmatrix} -1 & 1 & 0 \\ 2 & -1 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$
I supporti del T-vettore invariante y sono
$$ ||y|| = \{ t_1 \: t_2 \: t_3 \} $$
Si tratta di un vettore T-invariante minimale perché non esiste un altro vettore T-invariante inferiore y'<y
Ad esempio, tutti i vettori non nulli minori di y non sono T -invarianti.
$$ C \cdot [1,0,0]^T = [-1, 2] \\ C \cdot [0,1,0]^T = [1, -1] \\ C \cdot [0,0,1]^T = [0, -1] \\ C \cdot [1,1,0]^T = [0, 1] \\ C \cdot [1,0,1]^T = [-1, 1] \\ C \cdot [0,1,1]^T = [1, -2] $$
Nella rete esistono altri vettori T-invarianti non minimali.
Ad esempio il vettore y'=[2 2 2] è T-invariante ma non è minimale perché non è y'<y.
$$ \begin{pmatrix} -1 & 1 & 0 \\ 2 & -1 & -1 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$
Nota. Il vettore T-invariante y'=[2 2 2] si può ottenere come combinazione lineare del vettore T-invariante minimale y=[1 1 1]. $$ y'= \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} = a \cdot y $$ $$ y'= \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} = a \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} $$ con i coefficienti interi a=[2,2,2]T.
E così via.
