Insieme di raggiungibilità della rete di Petri

L'insieme di raggiungibilità della rete contiene tutte le marcature raggiungibili a partire dalla marcatura iniziale M0. $$ R(N,M_0) $$

Un esempio pratico

Ho la seguente rete di Petri con un grafo di raggiungibilità finito.

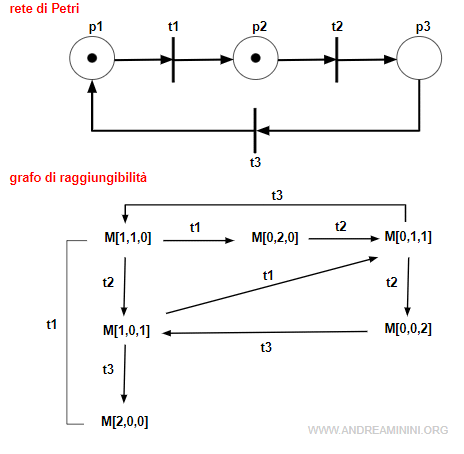
Dove

$$ M_0 = [1,1,0] \\ M_1 = [1,0,1] \\ M_2 = [2,0,0] \\ M_3 = [0,2,0] \\ M_4 = [0,1,1] \\ M_5 = [0,0,2] $$

Quindi, l'insieme di raggiungibilità R a partire dalla marcatura iniziale M₀ è composto dalle seguenti marcature:

$$ R(N,M_0) = \{ M_1, M_2, M_3, M_4, M_5 \} $$

Osservazioni

Se l'insieme di raggiungibilità è finito, si possono fare le seguenti osservazioni sul grafo di raggiungibilità della rete di Petri:

• Se una marcatura M è raggiungibile da M₀, ossia appartiene all'insieme di raggiungibilità R(N,M₀), allora la marcatura M è anche un nodo del grafo di raggiungibilità. E viceversa. $$ M \in R(N,M_0) \Leftrightarrow \text{M è un nodo} $$
• Se la marcatura M appartiene all'insieme di raggiungibilità R(N,M₀), allora esiste una sequenza di transizioni σ=t₁·t₂···t_n ossia un cammino orientato nel grafo che congiunge M₀ con M. Questa sequenza appartiene al linguaggio L(N,M) della rete.

  Esempio. Il nodo M₅ appartiene all'insieme di raggiungibilità . Quindi esiste almeno un cammino orientato da M₀ a M₅. Ad esempio, la transizione σ=t₁·t₂·t₂ collega la marcatura iniziale M₀ a M₅.
  
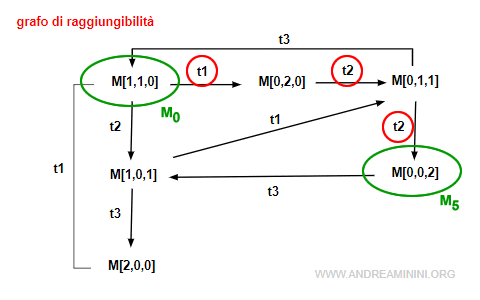
  Ovviamente, nel grafo possono esistere anche diversi cammini orientati alternativi ( es. σ=t₂·t₁·t₂ ). Non è detto che sia uno solo. Infine, se ci sono dei cicli lungo il cammino, il numero dei cammini orientati possibili potrebbe diventare infinito.

• Se la marcatura M' è raggiungibile dalla marcatura M e quest'ultima appartiene all'insieme di raggiungibilità R(N,M₀), allora anche M è un nodo del grafo di raggiungibilità ed esiste un cammino orientato da M a M'. Pertanto anche la marcatura M'∈R(N,M₀).

  Esempio. La marcatura M₂ è raggiungibile dalla marcatura M₅ tramite la sequenza di transizioni σ=t₃·t₃ ed esiste un cammino orientato da M₅ a M₂.
  

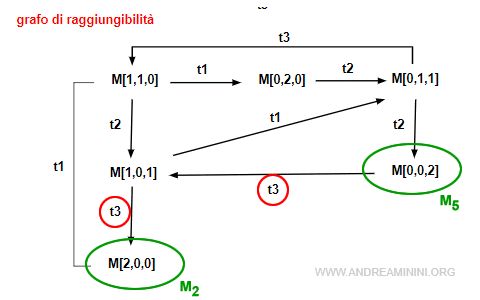
• Se una transizione t è abilitata da una marcatura M∈R(N,M₀) allora dal nodo M del grafo esce un arco con l'etichetta t.

  Esempio. Nella rete di Petri la marcatura M₁=[1,0,1] abilita le transizioni t₁ e t₃. Nel grafo di raggiungibilità dal nodo M₁=[1,0,1] escono due archi con etichette t₁ e t₃.
  

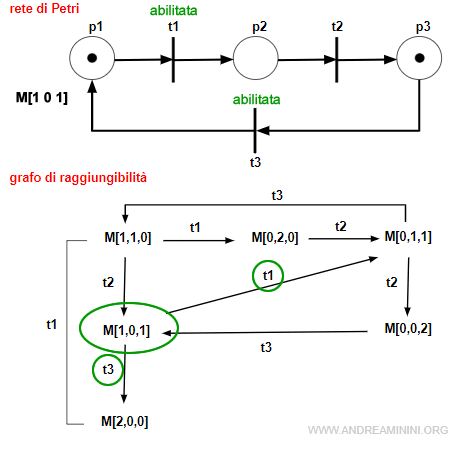
E così via