Legge di conservazione delle marche in una rete di Petri
- Data una rete marcata <N,M0> e un P-vettore
- se P-vettore è invariante (xI) il numero delle marche della rete è sempre costante. $$ x_I^T \cdot M_K = x_I^T \cdot M_0 $$
- se il vettore P è crescente (xC) il numero delle marche può crescere. $$ x_C^T \cdot M_K \ge x_C^T \cdot M_0 $$
- se il vettore P è decrescente (xD) il numero delle marche può decrescere. $$ x_D^T \cdot M_K \le x_D^T \cdot M_0 $$ per ogni marcatura raggiungibile Mk dalla marcatura iniziale M0
Un esempio pratico
Questa rete marcata ha tre posti e tre transizioni.
La marcatura iniziale M0 è [1 0 0]
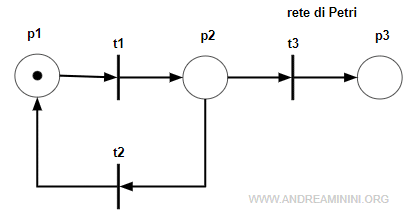
Calcolo la matrice di incidenza della rete tramite la differenza tra la matrice Post e Pre transizione.
$$ C = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} - \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{pmatrix} = $$
$$ C = \begin{pmatrix} -1 & 1 & 0 \\ 1 & -1 & -1 \\ 0 & 0 & 1 \end{pmatrix} $$
Esiste un vettore P invariante xI=[1 1 0] tale che
$$ x_I^T \cdot C = 0 $$
$$ \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} ^T \cdot \begin{pmatrix} -1 & 1 & 0 \\ 1 & -1 & -1 \\ 0 & 0 & 1 \end{pmatrix} = ( 1 \: 1 \: 0 ) \cdot \begin{pmatrix} -1 & 1 & 0 \\ 1 & -1 & -1 \\ 0 & 0 & 1 \end{pmatrix} = 0 $$
Il vettore invariante xI=[1 1 0] vuole dire che ogni sequenza di transizioni tra i posti p1 e p2 non modifica il numero delle marche della rete.
Questi due posti sono compresi nella seguenza σ=t1t2
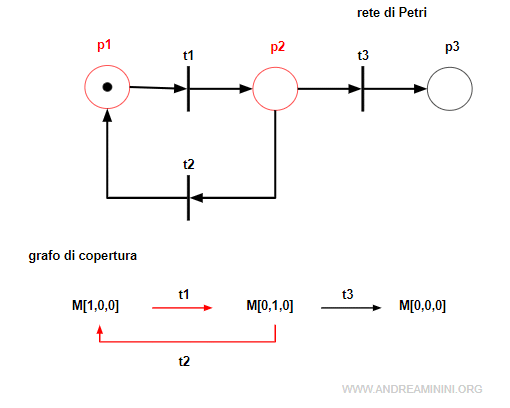
Pertanto, se ripeto k volte la sequenza σ=t1t2 il numero delle marche della rete è costante ed è pari a 1.
Nota. Se il P-vettore x fosse stato crescente, il numero delle marche della rete sarebbe aumentato. Viceversa, se decrescente sarebbe diminuito.
La dimostrazione
Prendo in considerazione una marcatura Mk raggiungibile da M0 con una sequenza σ=tj1tj2...tjk
$$ M_0[t_{j1}>M_1[t_{j2}>M_2 ... [t_{jk}>M_k $$
Una marcatura Mk+1 è raggiungibile da Mk con una sequenza tjk+1
$$ M_{k+1} = M_k + C \cdot t_{jk+1} $$
Posso scrivere la sequenza di transizioni tjk+1 come un vettore e di base canonica con n elementi tante sono le transizioni della rete.
$$ M_{k+1} = M_k + C \cdot e_{jk+1} $$
Esempio. Se la rete marcata ha quattro transizioni, la sequenza t1t3 equivale al vettore e=[1,0,1,0]. Ogni elemento del vettore indica il numero degli scatti per ogni transizione. In questo modo posso moltiplicare la matrice di incidenza C per il vettore di base canonica e.
Prendo un vettore x con m elementi, tanti quanti sono i posti e lo moltiplico per entrambi i membri.
$$ x^T \cdot M_{k+1} = x^T \cdot ( M_k + C \cdot e_{jk+1} ) $$
$$ x^T \cdot M_{k+1} = x^T \cdot M_k + x^T \cdot C \cdot e_{jk+1} $$
Se il vettore x è P-invariante, il prodotto xT·C=0
$$ x^T \cdot M_{k+1} = x^T \cdot M_k + ( x^T \cdot C ) \cdot e_{jk+1} $$
$$ x^T \cdot M_{k+1} = x^T \cdot M_k + 0 \cdot e_{jk+1} $$
$$ x^T \cdot M_{k+1} = x^T \cdot M_k $$
Pertanto, dopo lo scatto il numero delle marche della rete non cambia.
Questo risultato conferma la legge di conservazione delle marche.
E così via.
