Reti duali
Data una rete P/T con m posti e n transizioni detta primale $$ N=(P,T,Pre,Post) $$ la sua rete duale è una rete con n posti e n transizioni $$ N^T = ( T,P,Pre^T,Post^T) $$ Le matrici Pre e Post della rete duale sono uguali alle rispettive matrici trasposte della rete primale.
La matrice di incidenza della rete duale è la matrice trasposta della matrice di incidenza della rete primale.
Si tratta di un'osservazione ovvia perché la matrice di incidenza di una qualsiasi rete dipende dalle sue matrici Pre e Post.
Nota. Se la rete A ha come rete duale la rete B allora la rete B ha come rete duale la rete A. La dualità è una relazione biunivoca.
Un esempio pratico
Questa rete primale N ha 4 posti e 3 transizioni
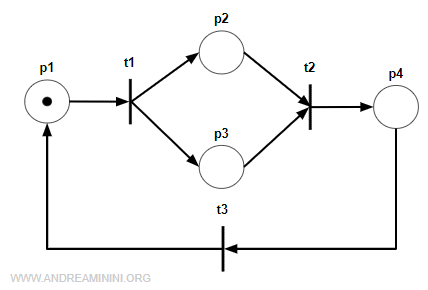
Le sue matrici Pre e Post sono le seguenti:
$$ Pre = \begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix} $$
$$ Post = \begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} $$
La sua matrice di incidenza è pari alla differenza delle matrici Post-Pre
$$ C = Post - Pre = \begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} - \begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix} $$
$$ C = Post - Pre = \begin{pmatrix} -1 & 0 & 1 \\ 1 & -1 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{pmatrix} $$
La sua rete duale ND ha 3 posti e 4 transizioni
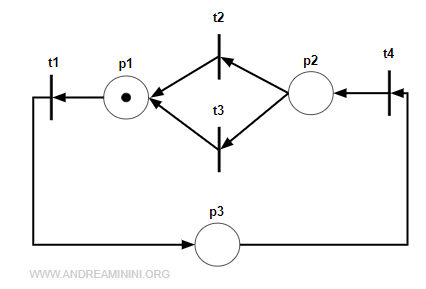
con le matrici Pre e Post trasposte rispetto alla primale
$$ Pre^T = \begin{pmatrix} -1 & 0 & 0 & 0 \\ 0 & -1 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} $$
$$ Post^T = \begin{pmatrix} 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{pmatrix} $$
Quindi, la matrice di incidenza della rete duale è la trasposta della matrice di incidenza della rete primale
$$ C^T = Post^T - Pre^T = \begin{pmatrix} 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{pmatrix} - \begin{pmatrix} -1 & 0 & 0 & 0 \\ 0 & -1 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} $$
$$ C^T = Post^T - Pre^T = \begin{pmatrix} -1 & 1 & 1 & 0 \\ 0 & -1 & -1 & 1 \\ 1 & 0 & 0 & -1 \end{pmatrix} $$
Nota. La matrice di incidenza della rete primale è $$ C = \begin{pmatrix} -1 & 0 & 1 \\ 1 & -1 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{pmatrix} $$ Essendo trasposte, le due matrici C e CT hanno le righe al posto delle colonne e viceversa.
Come costruire una rete duale
- Per determinare la rete duale di una rete P/T (primale)
- Sostituisco i posti con le transizioni
- Sostituisco le transizioni con i posti
- Inverto il verso degli archi
Il risultato finale è la matrice duale.
Esempio
Prendo in considerazione questa rete primale con 4 posti e 3 transizioni.

Sostituisco i posti con le transizioni e le transizioni con i posti.
Poi inverto il verso degli archi.

Ho così ottenuto la rete duale.
Nota. In questo esempio ho usato un grafo marcato come rete primale. La sua rete duale è una macchina di stato. Tuttavia, la rete duale si può costruire con qualsiasi rete. Non soltanto nel caso dei grafi marcati e delle macchine di stato.
E così via.
