La composizione concorrente delle reti di Petri
Date due reti di Petri etichettate N1 e N2, la composizione concorrente delle reti N3 si ottiene fondendo le transizioni che hanno la stessa etichetta. $$ L(N_3)= L(N_1)||L(N_2) \\ L_m(N_3)= L_m(N_1)||L_m(N_2) $$
La composizione concorrente di due moduli, sincronizza le transizioni appartenenti a moduli diversi che hanno la stessa etichetta.
Le due transizioni sono fuse in un'unica transizione composta che scatta soltanto se è abilitata da entrambi i moduli.
In questo modo, le transizioni sincronizzate scattano simultaneamente.
Nota. La composizione concorrente può essere realizzata anche con più di due transizioni sincrone.
Un esempio pratico
Ho due reti di Petri etichettate G1 e G2
$$ G_1 = (N_1, l_1, m_{0,1}, F_1 ) $$
$$ G_2 = (N_2, l_2, m_{0,2}, F_2 ) $$
Ecco la rappresentazione grafica dei due moduli
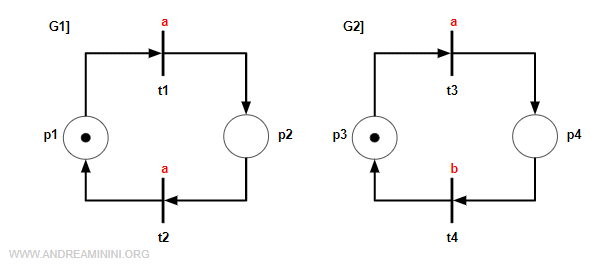
Ogni modulo ha un linguaggio che associa un'etichetta alle transizioni.
Il linguaggio di Petri del primo modulo è
$$ l_1 (t_1) = a \\ l_1 (t_2) = a $$
Il linguaggio di Petri del secondo modulo è
$$ l_2 (t_3) = a \\ l_2 (t_4) = b $$
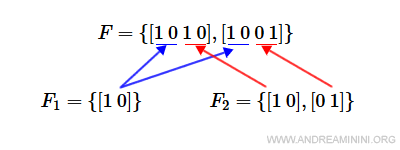
Gli stati finali delle reti sono
$$ F_1 = \{ [1 \: 0] \} $$
$$ F_2 = \{ [1 \: 0], [0 \:1] \} $$
A questo punto comincio a costruire la loro composizione concorrente
$$ G = G_1 || G_2 $$
Le transizioni t1, t2 e t3 hanno la stessa etichetta "a".
Quindi, sono sincrone e le posso unire in un'unica transizione composta.
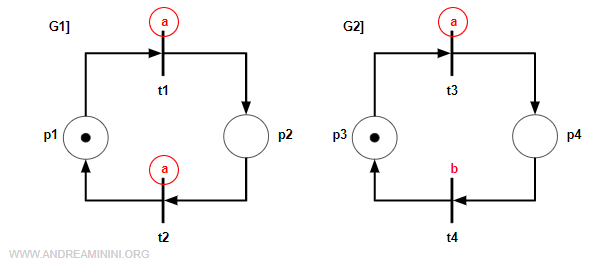
Nota. Soltanto le coppie t1-t3 e t2-t3 appartengono a moduli diversi. La transizioni t1 e t2 hanno la stessa etichetta ma appartengono alla stesso modulo. In questo caso, quando due transizioni nello stesso modulo hanno la stessa etichetta, devo comporre tutte le possibili combinazioni con le transizioni dell'altro modulo di pari etichetta. Quindi t1-t3 e t2-t3.
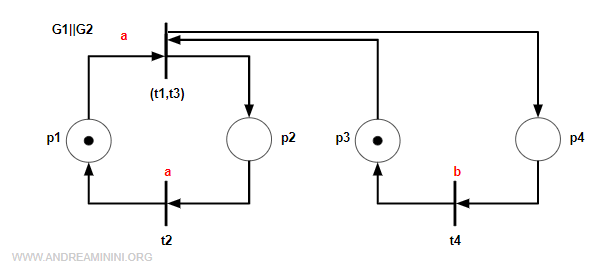
Unisco le transizione a coppia.
Comincio con le transizioni t1 e t3. Le unisco in una transizione composta (t1,t3).
Poi fondo le transizioni t2 e t3 in una transizione composta (t2,t3).
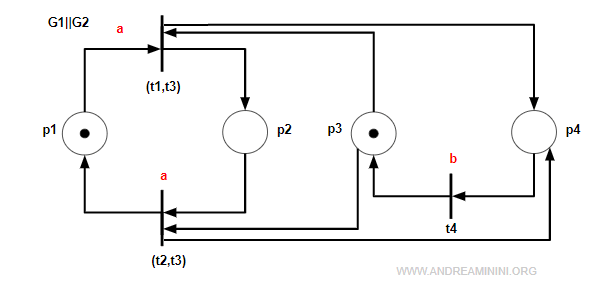
La marcatura iniziale m0 della composizione concorrente è
$$ m_0 = [1 \: 0 \: 1 \: 0] $$
Nota. Dove le posizioni del vettore m0 indicano le marche nei posti [ p1 p2 p3 p4]. Essendoci due marche, una in p1 e l'altra in p3, il vettore m0 diventa [1 0 1 0]
Gli stati finali sono le possibili combinazioni di F1 e F2.
Il vettore F è composto da due elementi.
$$ F = \{ [1 \: 0 \: 1 \: 0] , [1 \: 0 \: 0 \: 1] \} $$
Nota. Le posizioni del vettore F indicano i posti [ p1 p2 p3 p4]. I due elementi hanno i primi due posti uguali in p1 e p2 perché F1=[1,0]. Il terzo e il quarto posto in p3 e p4 cambia perché F2 è sia [1,0] che [0,1].
La complessità della composizione concorrente
La rete di Petri per composizione concorrente è composta dall'unione dei posti dei moduli
$$ |P|=|P_1|+|P_2| $$
e dalle combinazioni delle transizioni con la stessa etichetta tra i due moduli.
Se ciascun modulo non ha etichette ripetute tra due o più transizioni, il numero delle transizioni è
$$ |T| \le |T_1|+|T_2| $$
Quindi la fusione di k moduli comporta la creazione di n vertici (archi) nel grafo
$$ n = k \cdot (|T_1|+|T_2|) $$
Pertanto, si può affermare che la complessità della rete di Petri composta cresce in modo lineare con il numero k dei moduli che la compongono.
E questo è un bel vantaggio delle reti di Petri perché evita l'esplosione dello spazio degli stati.
Nota. In un generico sistema composto lo spazio degli stati spesso cresce in modo esponenziale. L'uso delle reti di Petri mi permette di evitare questo problema.
Va comunque detto che, se ci sono etichette ripetute in più transizioni in uno stesso modulo diventa molto più complesso.
E così via.
