La teoria degli insiemi

La teoria degli insiemi si basa sull'utilizzo del concetto di insieme nel linguaggio logico-matematico.

La definizione di insieme

Un insieme è una collezione di oggetti, detti elementi o membri, accomunati da una particolare proprietà. E' anche detto classe, aggregato o famiglia.

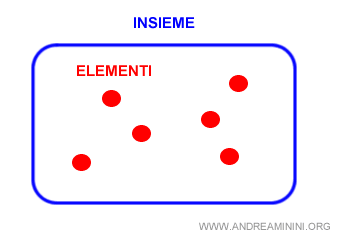
Si tratta di un concetto primitivo perché non è possibile definire l'insieme richiamando altri concetti.

In un insieme non è importante l'ordine degli elementi.

La definizione di insieme in matematica

In matematica un insieme è un raggruppamento di oggetti se esiste un criterio oggettivo che determina l'appartenenza o meno di qualsiasi oggetto al raggruppamento.

Quando si parla di insieme matematico si considera un particolare insieme in cui tutti gli oggetti soddisfano un criterio di appartenenza oggettivo.

Non sono insiemi matematici, invece, gli insiemi caratterizzati da criteri soggettivi.

Da questo momento in poi quando parlo di "insieme" intendo gli insiemi matematici.

Esempio. L'insieme dei numeri primi è un insieme matematico perché il criterio di appartenenza è oggettivo. Vi appartengono tutti i numeri naturali che sono divisibili solo per 1 e per se stessi. $$ I = \{ 2 , 3, 5, 7, 11, ... \} $$ Viceversa, l'insieme delle canzoni più belle non è un insieme matematico perché il criterio di appartenenza è soggettivo. Cambia da persona a persona.

La rappresentazione degli insiemi

Nel linguaggio logico-matematico gli insiemi sono indicati da lettere maiuscole ( A, B, C, D, ... ).

Gli elementi dell'insieme sono invece indicati con le lettere minuscole ( a, b, c, d, ... ).

I simboli di appartenenza e non appartenenza

Il simbolo di appartenenza a un insieme è ∈.

Si legge "l'elemento x appartiene all'insieme A".

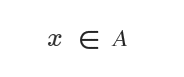
Il simbolo di non appartenenza a un insieme è ∉.

Si legge "l'elemento x NON appartiene all'insieme A".

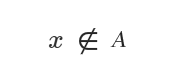
Esempio. Considero l'insieme B dei numeri pari da 1 a 9. $$ B = \{ \ 2 \ , \ 4 \ , \ 6 \ , \ 8 \ \} $$ Per indicare che il numero 2 appartiene all'insieme B scrivo $$ 2 \in B $$ Per indicare che il numero 3 NON appartiene all'insieme B scrivo $$ 3 \notin B $$

La rappresentazione grafica

Per rappresentare graficamente un insieme si usano i diagrammi di Eulero-Venn anche noti come cerchi di Eulero.

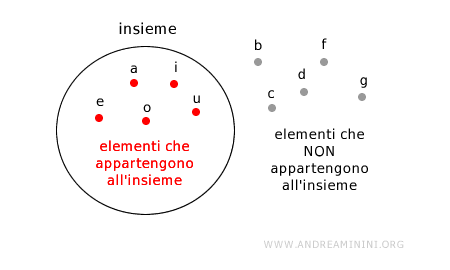
Ogni insieme è rappresentato da un cerchio, un ovale o una poligonale chiusa.

Gli elementi che appartengono all'insieme sono posti dentro il cerchio.

Quelli che non appartengono all'insieme, invece, si trovano al di fuori del cerchio.

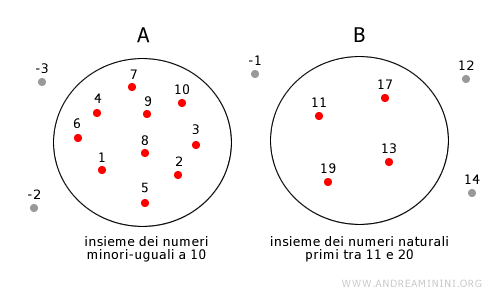
Nota. Nell'insieme A sono presenti i numeri naturali fino a 10. Tutti i numeri al di fuori del cerchio A non appartengono all'insieme A. Nell'insieme B invece sono racchiusi i numeri primi tra 11 e 20. Allo stesso modo, tutti i numeri che si trovano al di fuori del cerchio B non appartengono all'insieme B. I numeri che si trovano al di fuori di entrambi i cerchi (-1, -2, -3, 12, 14, ... ) non appartengono né all'insieme A, né all'insieme B.

Se un elemento appartiene a entrambi gli insiemi deve essere racchiuso in entrambi i cerchi.

Ad esempio, se l'insieme B fosse l'insieme dei numeri primi tra 1 e 20 dovrei rappresentare gli insiemi A e B facendoli intersecare.

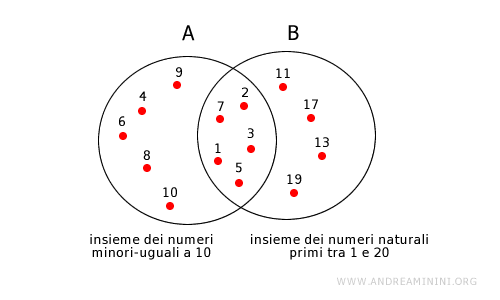
In questo caso gli elementi comuni a entrambi gli insiemi A⋂B={1, 2, 3, 5, 7} sono racchiusi sia in A che in B.

Nota. I diagrammi di Eulero-Venn prendono il nome del matematico svizzero Leonhard Euler e del matematico inglese John Venn che per primi li utilizzarono per indicare un insieme.

La rappresentazione elencativa o tabellare

Un insieme molto semplice può essere rappresentato anche in modo tabellare.

Nella rappresentazione tabellare scrivo tra parentesi graffe l'elenco degli elementi che appartengono all'insieme, separati tra loro da una virgola.

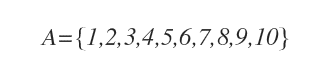
Questa rappresentazione è anche detta notazione elencativa.

Non è necessario indicare gli elementi secondo un ordine particolare. L'ordine degli elementi non ha importanza.

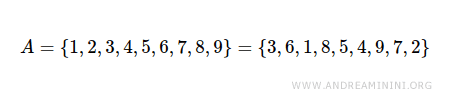
Gli eventuali elementi ripetuti nell'insieme vanno indicati una sola volta nella notazione elencativa.

Pertanto, non devono esserci elementi ripetuti più volte tra le parentesi graffe.

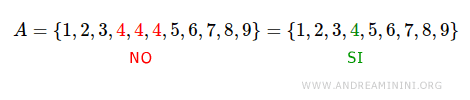
La rappresentazione tabellare è utile quando l'insieme è finito ed è composto da pochi elmenti.

E' invece scomoda quando l'insieme ha molti elementi.

Nota. A volte si utilizzano anche i puntini ... quando la regola di appartenenza all'insieme è abbastanza chiara e gli elementi non esplicitamente indicati sono comunque implicitamente comprensibili. Ad esempio, A={1,2,...,10} equivale a dire i numeri naturali da 1 a 10. $$ A = \{ \ 1,2, \ ... \ ,10 \ \} $$ Nella rappresentazione tabellare i puntini ... sono usati anche per indicare un insieme composto da infiniti elementi. Ad esempio A={1,2,3,...} equivale a dire tutti i numeri naturali da 1 in poi. $$ A=\{ \ 1,2,3 \ ... \ \} $$

La notazione comprensiva

Un insieme può essere anche rappresentato tramite una notazione comprensiva che si basa sulla regola o proprietà di appartenenza all'insieme.

Questa notazione è utile se l'insieme ha molti o infiniti elementi.

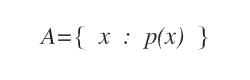
Tra le parentesi graffe va indicata la regola di appartenenza all'insieme, anche detta proprietà caratteristica, utilizzando il linguaggio formale della logica matematica.

Esempio. Nella notazione comprensiva numeri naturali da 1 a 10 sono rappresentati da A={x∈N:0<x≤10}.

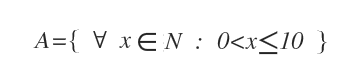
Dove x è una variabile che indica un numero naturale qualsiasi x∈N. Il simbolo ∀ si legge "per ogni". I due punti : si leggono "tale che". A volte si usa anche il simbolo | per indicare "tale che". $$ A = \{ \ \forall \ x \in N \ | \ 0<x \le 10 \} $$ Pertanto, la scrittura precedente si legge in questo modo: "A è l'insieme dei numeri naturali x tale che x è un numero tra 0 e 10".

Pro e contro delle notazioni

Posso usare la notazione comprensiva per rappresentare qualsiasi tipo di insieme, finito o infinito, purché gli elementi siano indivuabili da uno o più criteri.

La notazione elencativa posso invece usarla soltanto se:

• se un insieme finito è composto da pochi elementi
• se un insieme finito/infinito può essere rappresentato indicando esplicitamente soltanto alcuni elementi e sottintendere tutti gli altri.

Infine, la notazione grafica mi è utile soprattutto per spiegare o comunicare in modo visivo dei concetti altrimenti difficili da capire con la notazione logico-matematica.

Gli insiemi finiti e infiniti

Un insieme può essere finito o infinito.

• Un insieme finito è composto da un numero finito n di elementi.

  Esempio. L'insieme dei libri in uno zaino è un insieme finito. Un altro esempio di insieme finito è l'insieme dei granelli di sabbia in un recipiente.

• Un insieme infinito è composto da un numero infinito di elementi.

  Esempio. L'insieme dei numeri naturali è un insieme infinito, perché ogni numero naturale (n) ha un numero successore (n+1). Non esiste un numero naturale maggiore di tutti gli altri.

Gli insiemi numerici

Gli insiemi numerici sono insiemi composti da numeri

Per convenzione, in matematica gli insiemi numerici si scrivono con determinate lettere maiuscole.

• N è l'insieme dei numeri naturali
• Z è l'insieme dei numeri interi
• Q è l'insieme dei numeri razionali
• I è l'insieme dei numeri irrazionali
• R è l'insieme dei numeri reali
• C è l'insieme dei numeri complessi

L'insieme vuoto

L'insieme vuoto è un insieme senza elementi. Si indica con il simbolo Ø. $$ Ø = \{ \ \ \} $$

A volte l'insieme vuoto è indicato anche con due parentesi graffe senza alcun elemento.

E' un particolare insieme perché l'insieme vuoto è un sottoinsieme di qualsiasi altro insieme.

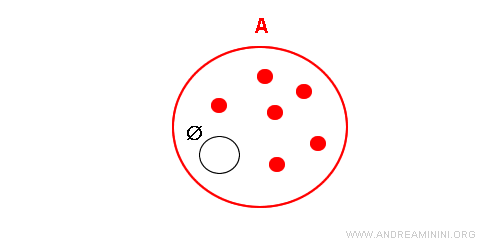
Esiste un solo insieme vuoto. Ad esempio, l'insieme dei numeri naturali dispari divisibile per due è un insieme vuoto perché nessun numero naturale dispari è divisibile per due. Anche l'insieme dei quadrati con tre lati è un insieme vuoto, perché ogni quadrato ha quattro lati. In entrambi i casi si tratta dello stesso insieme vuoto anche se il criterio di appartenenza è diverso.

E così via.