Gli estremi di un insieme
Cosa sono gli estremi
- Ogni insieme non vuoto ammette sempre un estremo superiore e inferiore.
- Negli insiemi limitati gli estremi sono numeri finiti.
- Negli insiemi illimitati gli estremi sono i simboli più o meno infinito (±∞).
Un insieme può anche essere limitato superiormente (estremo finito) e illimitato inferiormente (estremo infinito), o viceversa.
Nota. Gli estremi di un insieme possono appartenere o meno all'insieme.
Per capire questi concetti è utile approfondire la conoscenza degli estremi inferiori e superiori con degli esempi pratici.
L'estremo inferiore
Dato un insieme A e un sottoinsieme B non vuoto $$ B ⊆ A $$ l'estremo inferiore dell'insieme B è un elemento a∈A minore o uguale di ogni elemento di b∈B. $$ inf(B) = a \le b \:\:\: a \in A, b \in B $$
In altre parole, l'estremo inferiore è il più grande tra i minoranti dell'insieme B $ B $.
L'estremo inferiore di un insieme può appartenere o meno all'insieme stesso. Se appartiene all'insieme è detto minimo.
Ad esempio l'estremo inferiore di B è il numero 3.
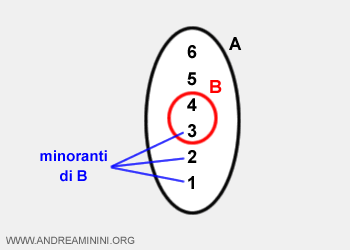
Negli insiemi limitati l'estremo inferiore è il massimo tra i minoranti.
Negli insiemi illimitati, invece, l'estremo inferiore è meno infinito (-∞).
Esempio 1
L'insieme A è l'insieme dei numeri reali R nell'intervallo (-∞,+∞).
L'insieme B è l'insieme di 7 numeri reali ed è un sottoinsieme di A.
$$ B = \{ 3, 4, 7, 5, 8, 9, 6 \} $$
L'estremo inferiore dell'insieme B è il numero tre
$$ inf(B) = 3 \le b \:\:\: \forall \: b \in B $$
perché è il numero reale 3 è minore-uguale a tutti gli elementi dell'insieme B.
Nota. In questo caso l'estremo inferiore inf(B)=3 appartiene all'insieme B. Non è detto però che sia sempre così.
Esempio 2
L'insieme A è l'insieme dei numeri reali R nell'intervallo (-∞,+∞).
L'insieme B è l'insieme dei numeri reali positivi R+ ed è un sottoinsieme di A.
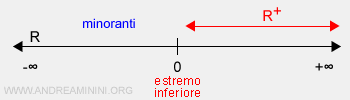
L'estremo inferiore dell'insieme B è il numero zero.
$$ inf(B) \le b \:\:\: \forall \: b \in B $$
E' il valore massimo tra i minoranti dell'insieme R+.
Nota. In questo caso l'estremo inferiore inf(B)=0 non appartiene all'insieme B (R+) perché tra lo zero e qualsiasi altro numero reale positivo, esistono altri infiniti punti.
L'estremo superiore
Dato un insieme A e un sottoinsieme B non vuoto $$ B ⊆ A $$ l'estremo superiore dell'insieme B è un elemento a∈A maggiore o uguale di ogni elemento di b∈B. $$ sup(B) = a \ge b \:\:\: a \in A, b \in B $$
In altre parole, l'estremo inferiore è il più piccolo tra i maggioranti di \( B \).
L'estremo superiore può appartenere o meno all'insieme stesso. Se appartiene all'insieme è detto massimo.
Ad esempio l'estremo superiore di B è 4.
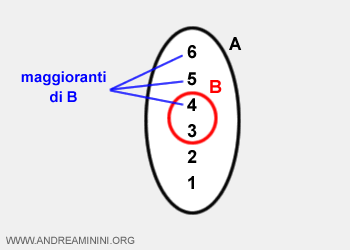
Negli insiemi limitati l'estremo superiore è il minimo tra i maggioranti.
Negli insiemi illimitati, invece, l'estremo superiore è più infinito (+∞).
Esempio 1
L'insieme A è l'insieme dei numeri reali R nell'intervallo (-∞,+∞).
L'insieme B è l'insieme di 7 numeri reali ed è un sottoinsieme di A.
$$ B = \{ 3, 4, 7, 5, 8, 9, 6 \} $$
L'estremo superiore dell'insieme B è il numero nove
$$ sup(B) = 9 \ge b \:\:\: \forall \: b \in B $$
perché è il numero reale 9 è maggiore-uguale a tutti gli elementi dell'insieme B.
Nota. In questo caso l'estremo inferiore sup(B)=9 appartiene all'insieme B. Non è detto però che sia sempre così.
Esempio 2
L'insieme A è l'insieme dei numeri reali R nell'intervallo (-∞,+∞).
L'insieme B è l'insieme dei numeri reali positivi R- ed è un sottoinsieme di A.
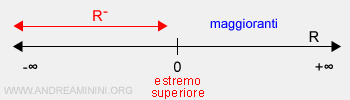
L'estremo inferiore dell'insieme B è meno infinito.
$$ inf(B) = - \infty \le b \:\:\: \forall \: b \in B $$
Nota. In questo caso l'estremo inferiore inf(B)=-∞ appartiene all'insieme B (R-) perché l'insieme reale negativo è illimitato inferiormente. Viceversa, l'estremo superiore sup(B)=0 non appartiene all'insieme B (R-) perché non è un numero reale negativo.
Gli estremi di un insieme reale
In alternativa l'estremo inferiore e superiore di un insieme reale possono essere definiti anche in questo modo:
Estremo inferiore di un insieme reale
Dato un insieme reale \( E \subset \mathbb{R} \) limitato inferiormente, si dice estremo inferiore di \( E \) il numero reale \( m \) tale che:
- per ogni \( x \in E \) si ha \( x \ge m \);
- per ogni \( \varepsilon > 0 \) esiste almeno un elemento \( x \in E \) tale che \( x < m + \varepsilon \).
In questo caso si scrive \( m = \inf E \).
Questa definizione esprime il fatto che \( m \) è il più grande tra tutti i minoranti di \( E \).
Estremo superiore di un insieme reale
Dato un insieme reale \( E \subset \mathbb{R} \) limitato superiormente, si dice estremo superiore di \( E \) il numero reale \( M \) tale che:
- per ogni \( x \in E \) si ha \( x \le M \);
- per ogni \( \varepsilon > 0 \) esiste almeno un elemento \( x \in E \) tale che \( x > M - \varepsilon \).
In questo caso si scrive \( M = \sup E \).
Questa definizione esprime il fatto che \( M \) è il più piccolo tra tutti i maggioranti di \( E \).
Note
Alcune note e osservazioni a margine
- Ogni sottoinsieme non vuoto dell’insieme dei numeri reali ammette estremo superiore ed estremo inferiore
In particolare, se un insieme è illimitato superiormente, il suo estremo superiore è \( \sup A = +\infty \). Analogamente, se un insieme è illimitato inferiormente, il suo estremo inferiore è \( \inf A = -\infty \). Se invece un insieme è limitato superiormente, allora possiede un estremo superiore finito, che è unico. Allo stesso modo, ogni insieme limitato inferiormente possiede un estremo inferiore finito, anch’esso unico. In questo senso, il concetto di estremo è sempre ben definito, purché si lavori nel contesto dei numeri reali estesi.Dove per "reali estesi" si intende l'insieme dei numeri reali $ \mathbb{R} $ a cui si aggiungono i simboli \( -\infty \) e \( +\infty \), che non sono numeri reali, per rendere sempre definibili l'estremo superiore e l'estremo inferiore.
E così via.
