Differenza tra insiemi
La differenza tra due insiemi A e B è un insieme (detto insieme differenza) composto dagli elementi dell'insieme A che non appartengono anche all'insieme B. $$ A-B = \{ x \ | \ x \ \in A \ ∧ \ x \notin \ B \} $$ Si legge "A meno B". Ecco il diagramma di Venn.
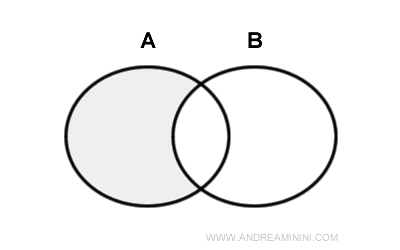
A volte la differenza tra gli insiemi è indicata anche in questo modo
$$ A \text{ \ } B $$
Si legge "l'insieme A\B è il complemento dell'insieme B".
Un esempio pratico
Considero due insiemi finiti A e B
$$ A = \{ 0, 2, 4, 8, 10 \} $$
$$ B = \{ 2, 4, 6, 12 \} $$
La differenza tra i due insiemi è un insieme A-B che contiene gli elementi di A che non appartengono anche a B
$$ A-B = A \text{ \ } B = \{ 0, 8, 10 \} $$
L'insieme differenza è composto dagli elementi di A non in comune con B ossia { 0, 8, 10}.
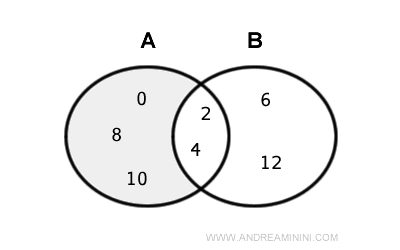
Gli elementi in comune tra i due insiemi, ossia 2 e 4, vanno tolti dall'insieme differenza.
Esempio 2
Considero due insiemi finiti A e B
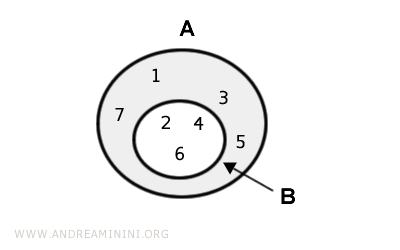
$$ A = \{ 1, 2, 3, 4, 5, 6, 7 \} $$
$$ B = \{ 2, 4, 6 \} $$
In questo caso l'insieme B è un sottoinsieme proprio dell'insieme A.
La differenza A-B è un insieme composto dagli elementi di A che non appartengono anche a B
$$ A-B = A \text{ \ } B = \{ 1, 3, 5,7 \} $$
L'insieme differenza è composto dagli elementi { 1, 3, 5, 7}.
Nella rappresentazione grafica tramite i diagrammi di Eulero-Venn l'insieme differenza è indicato in grigio.
Le proprietà della differenza
Alcune proprietà della differenza tra insiemi
- La differenza tra insiemi non è commutativa $$ A-B \ne B-A $$
Esempio. Considero due insiemi $$ A = \{ 0, 2, 4, 8, 10 \} $$ $$ B = \{ 2, 4, 6, 12 \} $$ La differenza A-B è $$ A-B = \{ 0, 8, 10 \} $$ mentre la differenza B-A è $$ B-A = \{ 6, 12 \} $$
- Se gli insiemi sono insiemi disgiunti, la differenza A-B coincide con il primo insieme A $$ A \cap B = Ø \Longleftrightarrow A-B= A $$
Esempio. Considero due insiemi $$ A = \{ 2, 4, 6, 8 \} $$ $$ B = \{ 1, 3, 5, 7. 9 \} $$ La differenza A-B è l'insieme A $$ A-B = A = \{ 2, 4, 6, 8 \} $$ Ecco la rappresentazione grafica
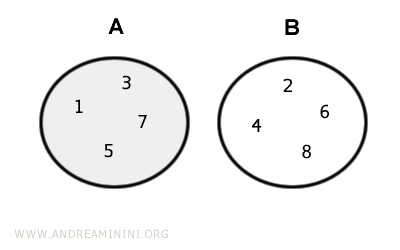
Allo stesso modo la differenza B-A è uguale all'insieme B $$ B-A = B = \{ 1, 3, 5, 7,9 \} $$ - Se gli insiemi sono insiemi uguali, la differenza A-B è l'insieme vuoto $$ A = B \Longleftrightarrow A-B= Ø $$
E così via.
